Question
(a) What is the distance between the slits of a diffraction grating that produces a first-order maximum for the first Balmer line at an angle of ?
(b) At what angle will the fourth line of the Balmer series appear in first order?
(c) At what angle will the second-order maximum be for the first line?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 53 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
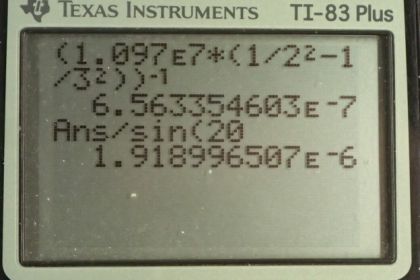
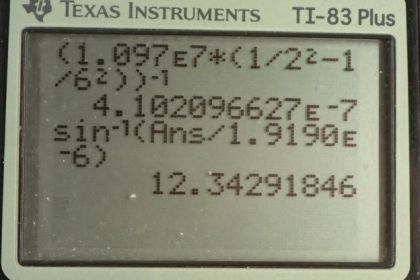
This is College Physics Answers with Shaun Dychko. Formula [27.3] tells us what the distance between slits and the diffraction grating must be to have a maximum at a certain angle, given a particular wavelength of light and m is the order of the maximum so each wavelength will give many maxima and we want to find the first one in part (a), in which case, m is 1. And we are told that the angle to this first maximum is 20 degrees and so what is d, the distance between the slits and we divide it by sin Θ on both sides to solve for d. Now the wavelength is something we have to figure out using equation [30.13] and we are asked in part (a) to use the first wavelength in the Balmer series for hydrogen. So we have the reciprocal of that wavelength is Rydberg's constant times 1 over the final energy level squared minus 1 over the initial energy level squared. And for the Balmer series, the final is 2 and the initial has to be more than the final in order for there to be a drop in energy level of the electron and therefore an emission of some photon of some energy. So n i has to be more than n f and so if we want the first wavelength, we'll take the first number greater than n f which is 3. So we plug in the number 3 here for n i. Now I solved for wavelength by taking the reciprocal of both sides which means raise both sides to the exponent negative 1 and this right-hand side, I just left it as wrapped in brackets with an exponent negative 1 because you know, getting a common denominator here and then flipping the fraction is more work than it's worth probably. So let's just do it like this. So we have the first wavelength in the Balmer series is Rydberg's constant— 1.097 times 10 to the 7 reciprocal meters— times 1 over the final energy level squared minus 1 over the initial energy level squared and all to the negative 1 giving us 656.34 nanometers. So that's the wavelength we plug in to this formula here to get the distance between the slits; the order is 1—it's the first maximum—times its wavelength divided by sin of 20 degrees which is 1.92 micrometers. Now in part (b), we are asked to figure out what will the angle be for the fourth line in the Balmer series? So n i has to be greater than n f; n f is definitely 2 because of the word 'Balmer', Balmer series and so n i can be 3, 4, 5, 6 and so on. And we want the fourth wavelength so that means n i is 6; number 3 would be the first, 4, 5, 6, 6 is the fourth. So that's why we plug in the number 6 there. And we rearranged this formula to solve for Θ now so Θ is the inverse sign of the order times the wavelength divided by the distance between the slits. And so we find out what the wavelength is by going Rydberg's constant times 1 over 2 squared minus 1 over 6 squared and then all to the negative 1 which is 410.21 nanometers. And then that wavelength is substituted in here and we are multiplying by 1 cause it's the first order maximum for this fourth wavelength in the Balmer series and dividing by the separation between the slits that we calculated in part (a); that number's written here times 10 to the minus 6 instead of the prefix 'micro' and then we are taking the inverse sign of all that to get the angle which is 12.3 degrees. And then part (c) says, at what angle will you find the second order maximum for the first wavelength in the Balmer series? So that means m is 2 and the wavelength is what we calculated up here— first wavelength in the Balmer series— and then dividing by the separation between the slits, taking the inverse sign of that and we get 43.2 degrees.