Question
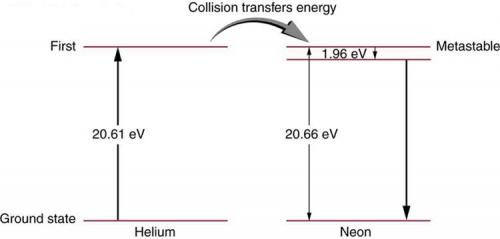
A helium-neon laser is pumped by electric discharge. What wavelength electromagnetic radiation would be needed to pump it? See Figure 30.39 for energy-level information.
<b>Figure 30.39</b> Energy levels in helium and neon. In the common helium-neon laser, an electrical discharge pumps energy into the metastable states of both atoms. The gas mixture has about ten times more helium atoms than neon atoms. Excited helium atoms easily de-excite by transferring energy to neon in a collision. A population inversion in neon is achieved, allowing lasing by the neon to occur.
Figure 30.39 Energy levels in helium and neon. In the common helium-neon laser, an electrical discharge pumps energy into the metastable states of both atoms. The gas mixture has about ten times more helium atoms than neon atoms. Excited helium atoms easily de-excite by transferring energy to neon in a collision. A population inversion in neon is achieved, allowing lasing by the neon to occur.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

60.2 nm60.2 \textrm{ nm}

Solution video

OpenStax College Physics for AP® Courses, Chapter 30, Problem 31 (Problems & Exercises)

OpenStax College Physics, Chapter 30, Problem 31 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 30, Problem 31 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. A helium-neon laser requires an energy to pump the helium atoms up to an energy state which is 20.61 electron volts and then these excited helium atoms will collide with a neon atom and cause its electron to go to a energy level that is 20.66 electron volts above the ground state and it's slightly higher than the excitation energy of the helium atom and the difference is 0.05 electron volts between these two numbers and that extra energy is supplied by thermal energy of the excited helium atom. And so the neon electron will go to this energy state here and then transition just a little bit down to this state here and from here, it will transition back to ground state and it's this transition that creates the photon that is emitted by the helium-neon laser. So the question is what incident wavelength photon is needed to excite these helium atoms? And so the energy of that photon will be Planck's constant times speed of light divided by wavelength and that energy is gonna be 20.61 electron volts cause we just need to excite these helium atoms. And then we can solve this for λ by multiplying both sides by 1 over λ or sorry, by λ, I should say and then divide by 20.61 and we get λ is hc over 20.61 electron volts. So that's 1240 electron volt nanometers— that's the product hc— and then the electron volts will cancel here; we divide that by 20.61 and we get 60.2 nanometers is the wavelength of photons needed to excite the helium atoms.