Question
Rutherford found the size of the nucleus to be about . This implied a huge density. What would this density be for gold?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 4 (Problems & Exercises)
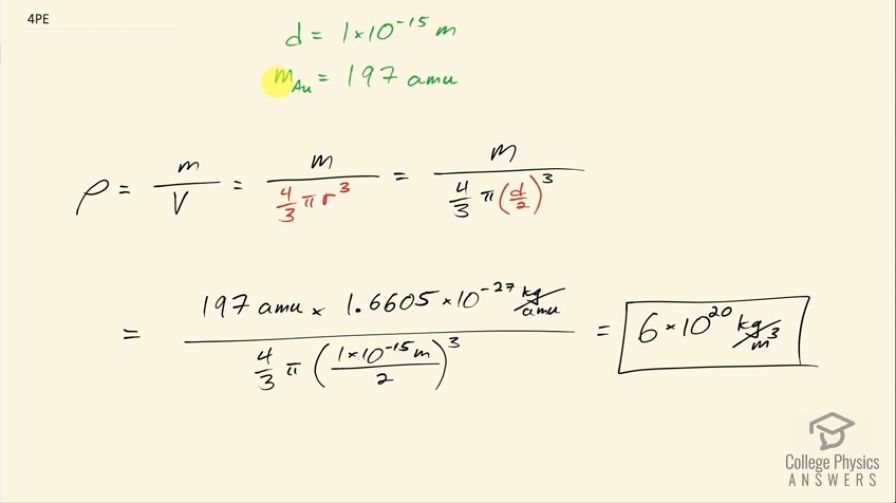
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The size of this nucleus is its diameter and it's about 1.00 times 10 to the minus 15 meters and we are asked to figure out what is the density for a gold nucleus then? So the mass of gold is 197 atomic mass units and I figured that out from this appendix at the end of the textbook— Appendix A— and for gold, it's 197 when you round it to the one's place here and that has units of atomic mass units and we can convert that into kilograms by multiplying by this conversion factor 1.6605 times 10 to the minus 27 kilograms per atomic mass unit. So we take that mass for a single gold nucleus and by the way this atomic mass, it includes the mass of the electrons that surround the nucleus but the electron mass is so negligible we'll just take this to be the nuclear mass. So we take that mass and divide it by the volume, which is a sphere, so that's four-thirds π times its radius which is half of 1 times 10 to the minus 15 meters and we cube that radius, this works out to 6 times 10 to the 20 kilograms per cubic meter taking only one significant figure here because our nuclear size has only one significant figure.
