Question
In a laboratory experiment designed to duplicate Thomson’s determination of , a beam of electrons having a velocity of enters a
magnetic field. The beam moves perpendicular to the field in a path having a 6.80-cm radius of curvature. Determine from these observations, and compare the result with the known value.
Final Answer
% error = 0.35%
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 58 (Problems & Exercises)
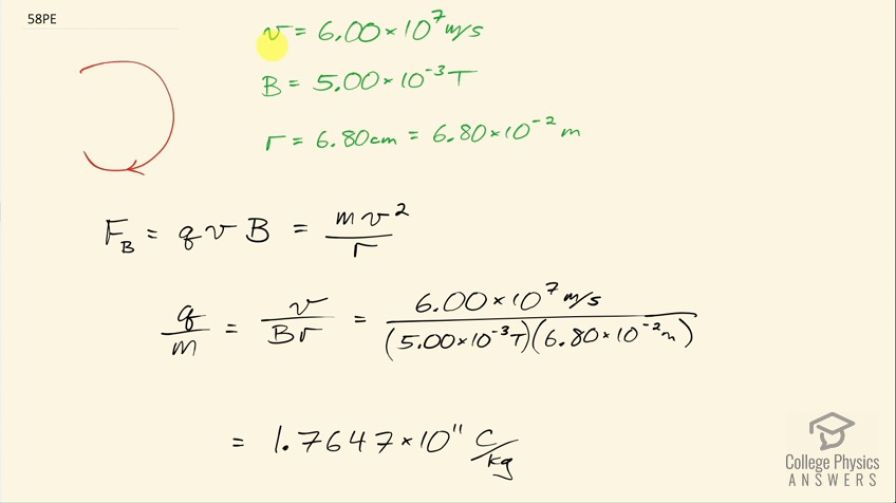
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A beam of electrons is moving in a circle in the presence of a magnetic field and the speed of the electrons is 6.00 times 10 to the 7 meters per second, the field is 5.00 times 10 to the minus 3 tesla and the radius of curvature of this path is 6.80 centimeters, which is 6.80 times 10 to the minus 2 meters. We are asked to figure out what is the ratio of charge to mass for these electrons? So the force due to the magnetic field is the charge times the charge speed times the magnetic field strength and we are told that the velocity and the magnetic field are perpendicular and so we don't need to consider... we don't need another factor here for the angle so it's just qvB is the strength of the magnetic field force and this is going to be the centripetal force because this particle is moving in a circle and the formula for that is mass times speed squared divided by radius of curvature. So we can divide both sides by v and also divide both sides by m and arrive at this q over... and also divide both sides by B by the way and then we have on the left, the v's and the B's cancel and we are left with q over m and on the right hand side, we have v to the power of 1 over B times r. So that's 6.00 times 10 to the 7 meters per second divided by 5.00 times 10 to the minus 3 tesla times 6.80 times 10 to the minus 2 meters and this is 1.7647 times 10 to the 11 coulombs per kilogram and suppose as the final answer, we should be rounding that to 1.76 times 10 to the 11 coulombs per kilogram. Then we are asked to compare this with the known value for this ratio and that is 1.602 times 10 to minus 19 coulombs divided by 9.11 times 10 to the minus 31 kilograms and that's this number here and then we'll find the percent difference. So we have our calculated value based on the measurement of speed and so on for this electron in the experiment minus the known ratio divided by the known ratio times 100 percent and that is 0.35 percent is the percent error in the experiment.

