Question
We have discovered that an electron’s orbit must contain an integer number of de Broglie wavelengths. Explain why, under ordinary conditions, this makes it impossible for electrons to spiral in to merge with the positively charged nucleus.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 30, Problem 16 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
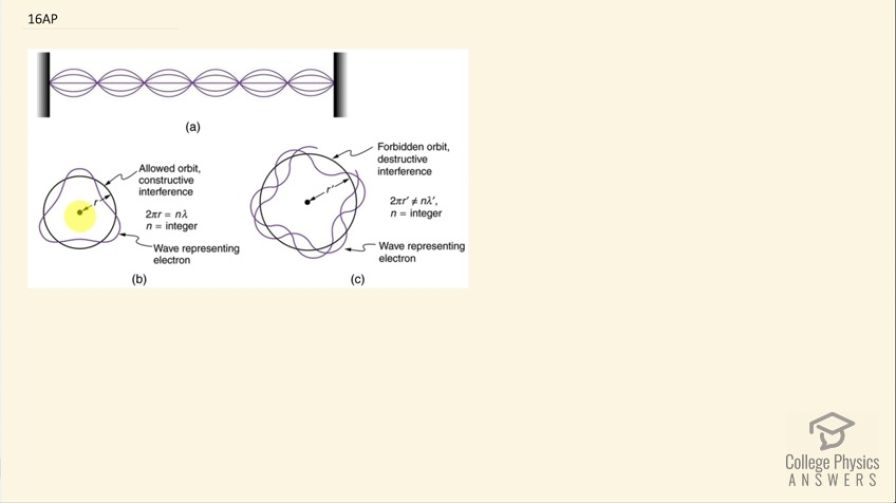
This is College Physics Answers with Shaun Dychko. An electron does not normally get into the nucleus in the center of the atom despite the fact that it is attracted to the nucleus because the nucleus is positive and the electron is negative but there is a process called electron capture where the electron does go into the nucleus and then it neutralizes one of the protons turning it into a neutron but normally that doesn't happen and that's a good thing because otherwise, you know, we would be left only with a world of neutrons. So we see that electrons do persist outside of the nucleus and the fact that they don't get captured normally is a good example of the wave nature of the electrons; these electrons are examples of resonance... the energy state of the electron around the nucleus is an example of resonance where only an integral number of the wavelength of the electron will fit in this space in the same way as the standing wave on a string requires an integral number of half wavelengths in order to fit between these n's in order to have a standing wave. Similarly, only an integral number of wavelengths of the electron will fit and so the electron can't go into the nucleus because then it would no longer be this example of resonance and it can't get any closer than n equals 1 because there is no number left in this sequence of 1, 2, 3, 4 and so on; these are the number of wavelengths that have to fit and the minimum you can get it is 1 and there is nothing that exists less than that. So... the orbitals or the energy states are going to transition discreetly from one number to the next— one number of wavelengths to the next— and that's the quantization is this idea of having discreet jumps between energy states— you can't have a continuous smear of energy from one state to the next— and so that's why in this picture here it's showing that if you have a wavelength that doesn't fit an integer number of times, it would be forbidden because there will be destructive interference in the same way that if you had a wavelength on this string that was not an integral number of half wavelengths the reflection from this end would interfere destructively with the incident wave going the other way and you'd not see the standing wave pattern. Okay... there we go! Hopefully that made some sense.