Question
(a) What is the width of a single slit that produces its first minimum at for 600-nm light? (b) Find the wavelength of light that has its first minimum at .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 46 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
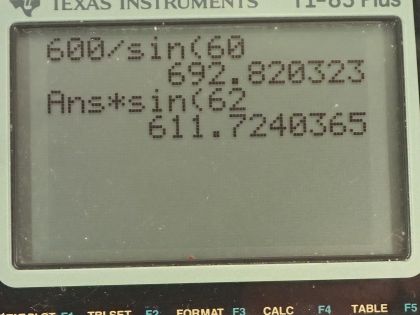
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. What is the width of a slit that produces its first minimum at an angle of 60 degrees when there is 600 nanometer wavelength light passing through the slit? This is our formula for the diffraction minima D is the width of a single slit, Θ is the angle to the minimum and m is the order of the minimum and λ is the wavelength and m could be any number— 1, negative 1, 2, negative 2 and so on— and it's important to remember that these are minima that we're talking about here and contrast that with the maxima in the similar looking formula for thin slit interference, which is this formula and that's not what we are dealing with here. Okay! So we want to find the width of the single slit and we are going to divide both sides by sin Θ to solve for D and so D then is the order times wavelength divided by the sin of the angle to the minimum. So it's the first minimum so that means m is 1 times 600 nanometers divided by sin of 60.0 degrees and that is 693 nanometers and the units are nanomete0rs since we have nanometers in our work here. And part (b) says well given this particular slit width, what wavelength would have its first minimum at 62 degrees? So we can solve this formula for λ by dividing both sides by m and we have λ then is the slit width times sin of the angle to the minimum divided by the order of the minimum. So that's 692.820 nanometers— that's the slit width written with more significant figures in order to avoid intermediate rounding error; we don't want to round numbers until we get our final answer. So we have the slit width times sin of 62.0 degrees that we're told divided by 1 and that is 612 nanometers is the wavelength of light that would have its first minimum at 62.0 degrees.