Question
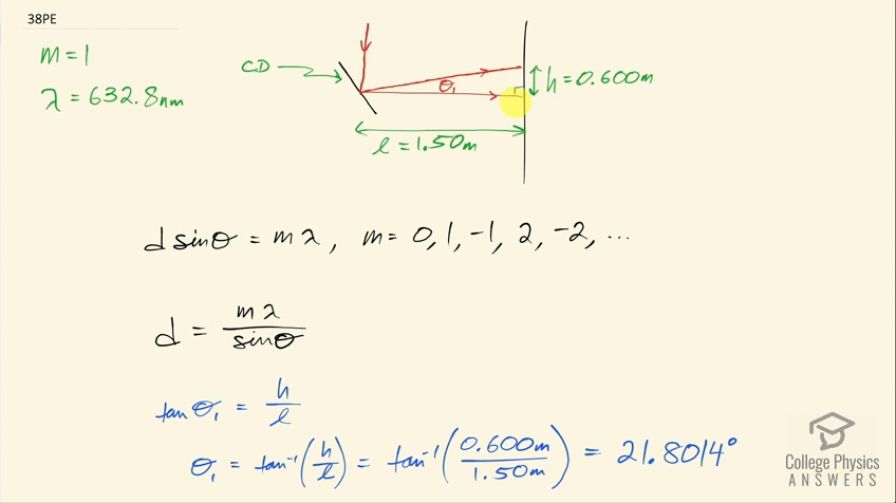
A He–Ne laser beam is reflected from the surface of a CD onto a wall. The brightest spot is the reflected beam at an angle equal to the angle of incidence. However, fringes are also observed. If the wall is 1.50 m from the CD, and the first fringe is 0.600 m from the central maximum, what is the spacing of grooves on the CD?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 38 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A helium-neon laser is shining on a CD and it reflects off onto the wall here and there's going to be a diffraction maximum some distance 0.600 meters above this sort of central reflection and this wall is 1.50 meters from where the CD is and we know the wavelength of this light we can look it up in Wikipedia wavelength for a helium-neon laser is 632.8 nanometers and since this is the first diffraction maximum that means the order is 1 and it's 1 in this formula here which tells us, you know, given the spacing between lines on the diffraction grating multiplied by sin of the angle to a maximum equals the order of the maximum times the wavelength and we can solve for d—the spacing between lines scratched on the CD— by dividing both sides by sin Θ and so d is mλ over sin Θ. So we need to know what Θ is and we have a right triangle here and the opposite is h and the adjacent is l and so that means tangent of this angle Θ 1— I put the subscript 1 here to say it's the angle to the first order maximum— equals the h over l then and that means the angle then is the inverse tangent of h over l take the inverse tan of both sides here (oops) so that's the inverse tan of 0.600 meters divided by 1.50 meters and that's 21.8014 degrees. So that's the number we use for Θ here and that means the spacing between lines then is the order 1 times the wavelength 632.8 nanometers divided by sin of 21.8014 degrees and that's 1703.87 nanometers and we know the units are nanometers since we used nanometers in our calculation here and then we can multiply by 1 micrometer for every 1000 nanometers just because this number looks nicer when expressed in units of micrometers and the answer is 1.70 micrometers.