Question
A soap bubble is 100 nm thick and illuminated by white light incident perpendicular to its surface. What wavelength and color of visible light is most constructively reflected, assuming the same index of refraction as water?
Final Answer
(green)
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 70 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
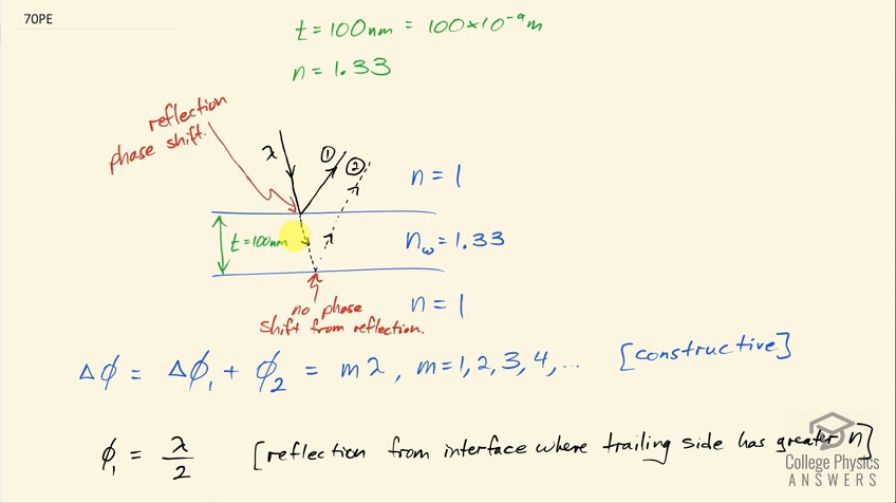
This is College Physics Answers with Shaun Dychko. Some white light is shining straight down on a soap bubble film and we are told that the inside of the film has an index of refraction close to that of water so it's 1.33 and inside the soap bubble, there's air so the index of refraction there is essentially 1 and on the outside of the soap bubble, the index of refraction is also 1 in air. So I have drawn this incident ray at a bit of an angle just in order to show in the drawing how there are two rays being reflected: one reflected off the first side of the soap bubble and the other ray being reflected off the inner edge of the soap bubble. And you know this ray is actually coming in straight down and these reflections are going straight back up and then they are overlapping because of that and then interfering with each other and we are going to be finding out what color has the greatest constructive interference but to draw them straight down and straight up, it would be too messy of a drawing so I am putting them on angles like this just to illustrate. We have ray number one reflected from the top surface and ray number two reflected from the bottom surface and we want to figure out what is the phase shift of each of these rays—ray one and ray two— and the total phase shift of the two of them has to be some integer multiple of the wavelength in order to have constructive interference. So I have this letter Φ to represent the phase shift and so we have a phase shift of this first ray and then a phase shift with the second ray. This first ray has a phase shift and we are measuring by the way we are measuring phase shift in terms of the number of wavelengths its shifted. Okay! So this interface here is an interface where the light is traveling in a low index of refraction 1 and then reflecting off an interface where the second medium is a higher index of refraction—1.33— and so when that happens there is an automatic phase shift of half of a wavelength and so that's why I have Φ 1 here equal to λ over 2 that's a reflection from an interface where the second side—the trailing side—has a greater index of refraction. And at this interface here, when the ray is traveling through the soap bubble in an index of refraction of 1.33, and then reflecting off this interface, there is no phase shift as a result of the reflection because the second medium, in this case, is the air inside the soap bubble, which has a lower index of refraction compared to where the light was starting before hitting this interface and it starts at 1.33. Okay! So there is a phase shift of this second ray though due to the additional distance that it's traveling and we need to figure out how many wavelengths is that distance? And the distance if you measured with a ruler would be 100 nanometers well, of course you can't use a regular ruler for that... that's pretty thin but the thickness of this soap bubble film we are told is 100 nanometers and we want to know how many wavelengths is that? Well, the question is not as simple as it seems because you can't take the wavelength that the light has in air, you need to take the wavelength that the light has in the bubble when figuring this out. So we have λ n which is to say the wavelength in this index in this medium that has some index of refraction n. So we take the distance that it's traveling additionally so this ray two is traveling this thickness twice and so we have 2 times t here— 2 times the thickness and how many wavelengths is that? Well we take that 2 times thickness divided by the wavelength in the soap film and then we take that and multiply it by the wavelength in air and this tells us the total phase shift in terms of the number of wavelengths. Okay! So the wavelength in the soap film is the wavelength in air or in a vacuum divided by the index of refraction in the soap film. Now we are dividing by λ n so I am going to instead multiply by the reciprocal of this fraction. So we have 2t times n of water divided by λ, these λ's cancel and so the phase shift of this second ray then is 2 times the thickness multiplied by the index of refraction of the water. So the total phase shift then is the phase shift of the first ray—λ over 2— plus the phase shift of the second ray, which is 2t times index of refraction and this has to equal some integer or natural number I should say multiplied by the wavelength in the air. We are going to try m equals 1 first of all... it could be 2 or 3 or so on... let's try m equals 1 and see if we end up with a visible wavelength, if we didn't, we would try a different value for m. So we have λ over 2 plus 2tn equals λ and we can subtract λ over 2 from both sides and then we end up with λ over 2 equals 2t times the index of refraction of water, multiply both sides by 2 and we have the wavelength then is 4 times the thickness times the index of refraction. So that's 4 times 100 nanometers times 1.33 and that is 532 nanometers. So this wavelength will experience constructive interference, it's the color green so it is visible and there we go!
