Question
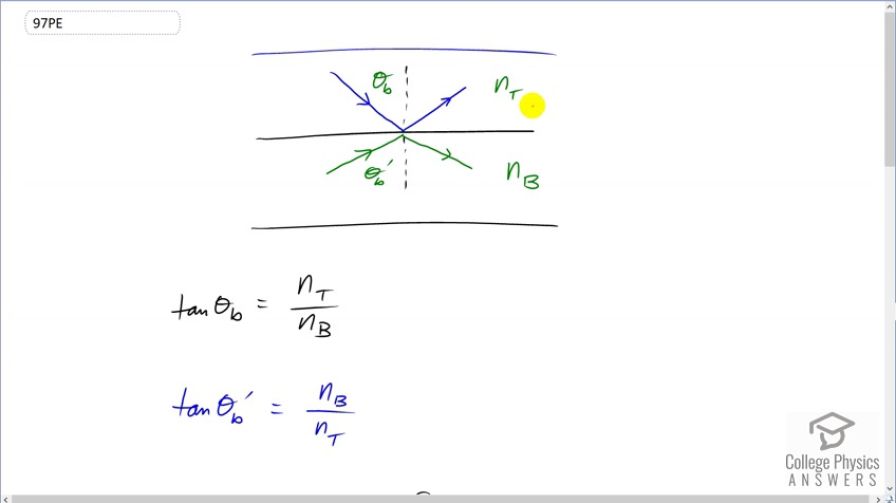
If is Brewster’s angle for light reflected from the top of
an interface between two substances, and is Brewster’s
angle for light reflected from below, prove that .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 97 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We have light incident through some medium that has an index of refraction n subscript ‘t’ for top and then it has some Brewster's angle theta b such that the reflected light is polarized. Now, if light were to approach this interface from the bottom and begin in this material with index of refraction n b and then reflect off of here polarized then we would call this Brewster's angle prime and our job in this question is to prove that theta b plus theta b prime is 90 degrees. So, we want to show that this is… this angle plus this angle is 90. Okay. So, tangent of Brewster's angle is the initial index of refraction divided by the final index of refraction and so for theta b it's going to be n top divided by n bottom. Now for the theta b prime, the formula will be n b because this is the material that it starts in, divided by n t which is the second material that it reflects off of. Now we can rearrange this theta b formula and solve for n t and then substitute that for n t in this expression here. So, we've multiply both sides of this by n b and we have n t is n b times tan theta b and then we substitute that in place of n t in this expression for a tan theta b prime. So, tan theta b prime equals n b divided by n b times tan theta b and the n b's cancel leaving us with one over tan theta b. So, if we multiply both sides by tan theta b, we see that the product of the tangent of each of the Brewster's angles equals one. Now tangent is the same as sine divided by cosine so tan theta b is sine theta b divided by cosine theta b and tan theta b prime is sine theta b prime divided by cosine theta b prime and all of this equals one still. Now we have a trigonometric identity to replace some things with here. We have cosine of one angle plus another equals cosine of the first times cosine of the second minus sine of the first time minus sign of the second. And for this expression we can rearrange it to say that sine theta b times sine theta b prime equals cos theta b times cos theta b prime. And now since this from what we have in blue here, equals this, we can substitute for the sine term here. So, sine theta b times sine theta b prime equals all of this which then gets plugged into there and we have that cosine of the sum of these angles is cosine of the theta b times cosine of theta b prime minus the same thing which is zero. And so, if we can take the inverse cosine now of this side and of zero, and we have that theta b plus theta b prime equals inverse cosine of zero and inverse cosine of zero is 90 degrees. Quod Erat Demonstrandum, all done.