Question
Repeat Exercise 27.71, but take the light to be incident at a angle.
Final Answer
The oil will appear black since visible wavelengths will not constructively interfere.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 82 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
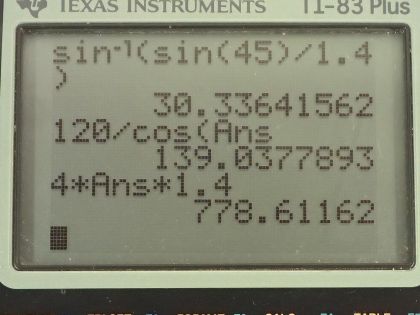
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An oil slick that is 120 nanometers thick is resting on some water and the oil slick has an index of refraction of 1.40 and water has an index of refraction of 1.33 and some light is incident at an angle of 45 degrees with respect to normal here and then when it crosses from this air-oil interface, it will refract towards the normal my drawing doesn't really show that but I am going to be calculating a different Θ r here for angle of refraction that's going to be different than the incident angle using Snell's Law and this should be directed towards the normal here in the picture but anyway this will do good enough here. So ray one will undergo a half wavelength phase shift due to the fact it's being reflected off of an interface where the second medium has a higher index of refraction than the first medium and ray two however will not experience phase shift due to reflection since it's going from a high index and then the second medium is a low index of refraction so this reflection does not have any phase shift due to reflection but there is a phase shift in ray two due to the increased path length that this ray has traveled compared to ray one. So we need to figure out what that additional path length would be and so we'll use Snell's Law to figure out what this Θ r is. We are given this thickness and then this is going to be the hypotenuse of a right triangle where the thickness is the leg adjacent to the angle Θ r and then find the hypotenuse of that triangle, multiply it by 2 and that will give us the additional path length for this second ray. Okay so that's the plan! The total phase shift is the phase shift due to ray one plus the phase shift due to ray two and in order for the color to be visible, this phase shift will have to result in constructive interference in which case you will have the phase shift total being some natural number times the wavelength and we are going to be calculating the different wavelengths for different values of m and see which color if any are going to be experiencing constructive interference. So the first ray experiences a phase shift of half of a wavelength and for the second ray, we are going to redraw this triangle here... this triangle here redrawn here... where d is the distance that the ray is traveling on its way down to the oil-water interface here and Snell's Law says that the index of refraction of the first medium times sin of the incident angle— that is the angle between the normal and the light ray— is going to equal the index of refraction of the second medium times sin of the angle in the second medium... angle of refraction. We are going to solve for sin Θ r first by dividing both sides by the index of refraction of the oil and get sin Θ r equals n air times sin Θ i over n oil and then take the inverse sin of both sides to get the angle of refraction. So that's going to be the inverse sin of 1 because the index of refraction of air is just 1 times sin of 45 degrees—incident angle— divided by 1.40—the index of refraction of oil— and this is 30.3364 degrees. So the cosine of this angle is the adjacent, which is the thickness that we are given divided by the hypotenuse, which is we want to find and that's what we have written here and we'll solve for d by multiplying both sides by d over cos of Θ r and then we get the distance then is the thickness divided by cos of Θ r. So that's 120 nanometers—thickness— divided by cos of 30.3364 degrees and that's 139.038 nanometers. Now the total additional path length of ray two is going to be 2 times that hypotenuse of that triangle and so we have 2d substituted in place of this additional path length. So this additional path length we have to express it in terms of the number of wavelengths that represents and we are going to divide that path length by the wavelength that exists inside the medium so that's why there's a subscript n there and then we multiply that by the wavelength back in the air. So the wavelength in the medium then is the wavelength in air or vacuum divided by the index of refraction in the oil and since we are dividing by this fraction, we are going to instead multiply by its reciprocal so I flipped this fraction over and multiply 2d by this flipped over. So the phase shift for ray two then is 2 times d—this hypotenuse here— times the index of refraction of oil divided by the wavelength in air or vacuum and this is 2dn then for the phase shift of ray two. So the total phase shift would be the phase shift due to ray one due to reflection there and then add to that this phase shift of ray two and that equals mλ we are solving for λ here we are going to subtract λ over 2 from both sides and then switch the sides around and we've mλ minus λ over 2 equals 2dn multiply this by 2 over 2 to get a common denominator of 2, factor out the λ and we have λ times 2m minus 1 over 2 and then multiply both sides by 2 over 2m minus 1 and we get the wavelength then is 4 times d times n over 2m minus 1; this n by the way is the index of refraction of oil— I wasn't being specific about that but that's what it represents here. Okay! So we have to try different values for m so let's try m equals to 1— that's the smallest possible value. So the first wavelength that experiences constructive interference is 4 times 139.038 nanometers times 1.40 divided by 2 times 1 minus 1 and that's 779 nanometers. The longest wavelength that's visible is about 760 nanometers and this exceeds that so that means it is not visible— this is infrared radiation here. Let's try a different value for m... let's try number 2. So λ 2 is going to be the same numbers here except we have the 2 substituted for m and this is 260 nanometers— this also is not visible, it is ultraviolet light— it is shorter wavelength than the shortest possible visible wavelength which is about 360 nanometers or so. So anyway... this oil will appear black because none of the colors that are visible will experience constructive interference.