Question
(a) Find the angle of the third diffraction minimum for 633-nm light falling on a slit of width . (b) What slit width would place this minimum at ? Explicitly show how you follow the steps in Problem-Solving Strategies for Wave Optics
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 50 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
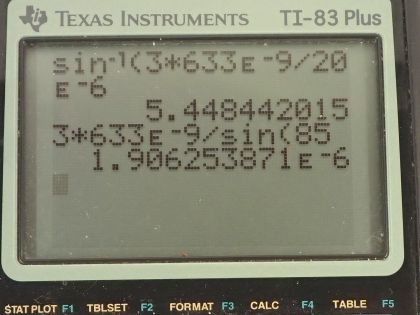
This is College Physics Answers with Shaun Dychko. We are going to find the angle to the third diffraction minimum when 633 nanometer light passes through a single slit of width 20.0 micrometers. We need to have the units the same here so we are going to change the nanometers into 633 times 10 to the minus 9 meters and replace the prefix 'micro' with times 10 to the minus 6 and so this is in meters as well. Here's our formula relating the slit width to the angle to the minimum and relating that to the order of the minimum and the wavelength of the light. So we can solve for sin Θ first of all by dividing both sides by the slit width so sin Θ is the order times the wavelength divided by the slit width and then take the inverse sin of both sides to solve for Θ. So Θ then is the inverse sin of the order times the wavelength divided by the slit width. So that's the inverse sin of 3 times 633 times 10 to the minus 9 meters divided by 20.0 times 10 to the minus 6 meters and that's 5.45 degrees. Now what slit width would place the same minimum at 85.0 degrees? So that means the order is the same and the wavelength is the same and only D is changing here so we can solve this for D by dividing both sides by sin Θ and we would get this formula here and I put a little subscript 3 here to say this is the angle to the third minimum and I put a prime here to say it's different than you know the third minimum that we had up here. I guess I could have put a subscript 3 on this one as well if I wanted to but I didn't bother at that time. Okay! So we plug in 3 for the order and 633 times 10 to the minus 9 meters is the wavelength and dividing by sin of this new angle for this 3rd order minimum— 85.0 degrees— and we get 1.9063 times 10 to the minus 6 meters, which is 1.91 micrometers.