Question
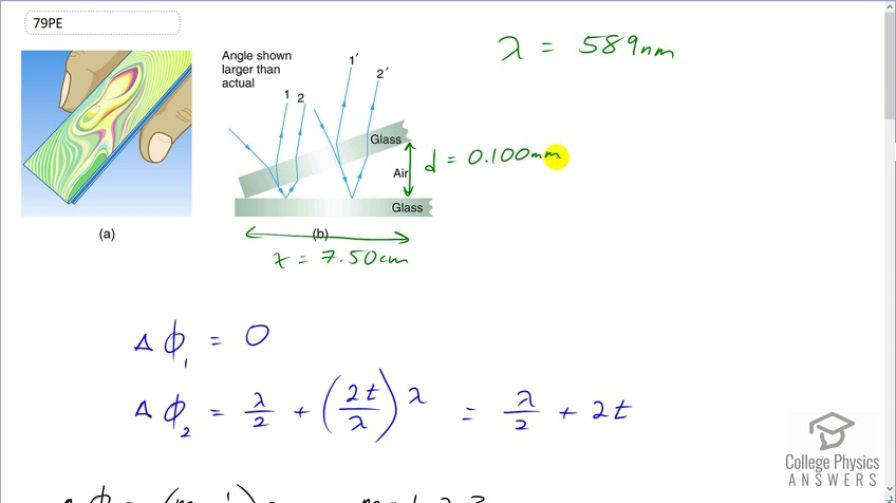
Figure 27.34 shows two glass slides illuminated by pure- wavelength light incident perpendicularly. The top slide touches the bottom slide at one end and rests on a 0.100-mm-diameter hair at the other end, forming a wedge of air. (a) How far apart are the dark bands, if the slides are 7.50 cm long and 589-nm light is used? (b) Is there any difference if the slides are made from crown or flint glass? Explain.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 79 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Two glass slides are separated at one end by a piece of hair that is 0.1 millimeters in diameter. And so the distance here is 0.1 millimeters. Then the pieces of glass are touching at this end. So this forms a triangular wedge of air between the pieces of glass. Now light incident here will interfere. It'll one Ray will bounce off of this interface between glass and air and then go upwards. And then the another Ray will bounce off the bottom piece of glass and then go back up. And this drawing is not quite accurate because it says that the light is incident perpendicularly. So all these rays are in fact overlapping but it would be too difficult to draw that and explain where the different rays are coming from. And so that's why it's showing an angle. But keep in mind that it's meant to be overlapping so rays one and two will interfere. And in this case because we're looking for dark bands the interference is going to be destructive. And then at some position later further down here some distance delta x you'll have the next dark band occurring when there is destructive interference again as a result of this increased path length difference. So let's figure out expressions for the phase shifts of Rays one and two and then and then we'll see how that changes with horizontal position. Now the phase shift of Ray one is zero because this reflection here occurs at an interface where you're beginning in a medium with high index refraction and some kind of glass and then going to a medium of low index refraction which is air. And so there is no phase shift there. And then for Ray two however there's a reflection off of this interface between the air in the glass and this does have a phase shift automatically of half of a wavelength when going from a low index refraction to a high index refraction and then additionally there's a phase shift due to this additional path length travelled by ray two. And so we calculate the number of wavelengths that path length corresponds to and then multiply by the wavelength. And this works well these are actually going to be the same because normally I have a subscript n here to say you know the additional path divided by the wavelength in that medium. But in this case the medium is air. So these cancel and we have a two there because the ray is going down once over that thickness and then up again over the thickness it's doing a round trip traveling that thickness twice the thickness of that air gap there. And this works out to Pi over two plus two times the thickness of the air gap. So now we have phase shifts for each of the two rays. Now the total phase shift when you add them together has to be some integer plus a half times the wavelength in order to have destructive interference and this total phase shift is going to be Delta Phi 1 plus Delta Phi 2 equals m plus half times wavelength. And now we can substitute these expressions for Delta Phi that we found before in blue zero four every one and then lambda over two plus 2t for ray two and we're going to solve this for t . And so I multiply both sides by two here and then distribute the lambda into the brackets and end up with Lambda plus 40 equals I guess I just multiplied the two into the brackets there. So that's 2m plus one times lambda and you end up with 2m lambda plus lambda and then subtract a lambda from both sides and you have 40 equals 2m lambda and then t is m lambda over two. So this is an expression for the thickness of the air gap needed to have destructive interference. And there will be many such thicknesses that cause destructive interference because we can choose any value any integer value for m. So we're going to have here's the use with the glass pieces are touching and that's some thickness t1 will have destructive interference. And that's at a horizontal position x1 from this point where they're touching and then again will have destructive interference that happening again at t2 . So this will be corresponding to m equals one and this corresponds to m equals two these two thicknesses. We would plug in the number one or the number two into this expression for thickness and this will happen at a position x2 . And the question is asking us what is the difference between these horizontal positions. How far apart are the dark bands horizontally. What is delta x in other words. So these are similar triangles and because the angles are all the same. I mean they share this common angle here and this is a 90 degree angles. That means this angles the same two and because they're similar that means that the ratio of corresponding sides is the same. So when you take x2 divided by t2 that's gonna be the same as x1 divided by t1 . So let's just call it x over d . And d being, this is, this here because we know what the ratio for this triangle is and the ratios where all the triangles inside here are all going to be the same because they're all similar. And I mean similar in a mathematical technical sense of the word meaning that all the time all the angles in the Triangle are the same and therefore ratios of corresponding sides are the same. And we know the opposite and the adjacent for this triangle here it's 0.1 millimetres high and 7.5 centimeters long. So we can say that x2 is t2 times x over d and x1 is t1 times x over d and we'll substitute for each of those in this expression for delta x. And that's what I've done here and the x over d can be factored out and it's gonna be t2 minus t1 times x over d and Delta x then substituting for t2 and t1 using this expression here substituting the numbers two and one for n . We have two times lambda over two minus one times lambda over two times x over d and then this works out to Lambda over two and then we can substitute in numbers. So that's 589 nanometres is the wavelength we told divided by two times seven and a half centimeters written as times ten to the minus two meters divided by 0.1 millimetres written as times ten to the minus three meters gives us this many nanometres which is 0.221 mm. So this is the horizontal separation between dark bands. Now what you would expect in this picture is to see lines like this spaced apart 0.221 millimeters and in reality though you don't see that because that's showing you that there are imperfections in these pieces of glass it means that they're not perfectly straight as shown in the drawing and so that's kind of interesting and this is one of the ways that they actually engineer really nearly perfect mirrors for telescopes and so on is by looking at interference patterns like this.
