Question
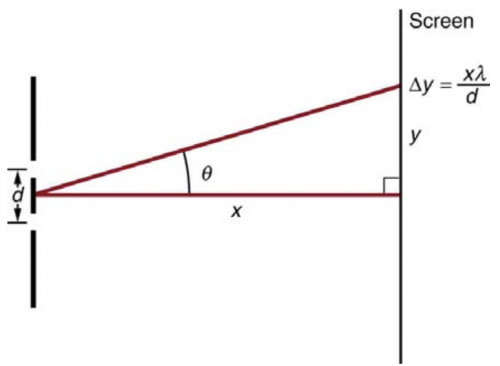
Figure 27.56 shows a double slit located a distance x from a screen, with the distance from the center of the screen given by . When the distance between the slits is relatively large, there will be numerous bright spots, called fringes. Show that, for small angles (where , with in radians), the distance between fringes is given by Δy = xλ / d .
Final Answer
Please see the solution video for the derivation.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
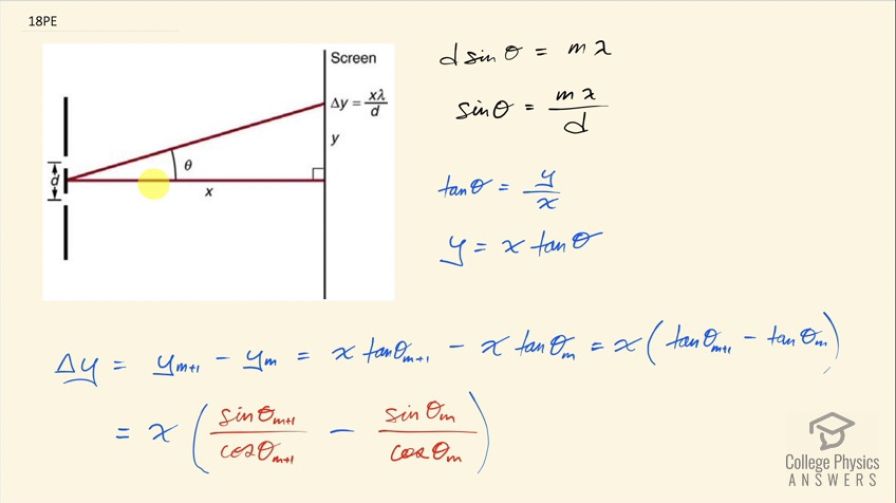
This is College Physics Answers with Shaun Dychko. We have a double slit interference pattern being shown on the screen and the screen is a distance x from the two slits, the slits are separated by a distance d and the distance to this bright fringe from the centered line here is y and we are meant to show that Δy— the distance between adjacent fringes— is this distance x times the wavelength of light divided by the separation between the slits d when we have a small angle Θ. Okay! So we have this formula for telling us where the constructive interference bright fringes are separation between slits times sin Θ equals the order of the fringe times the wavelength λ and we can solve this for sin Θ by dividing both sides by d and that's as far as we can go with that. This is going to be useful though... you know, we have a clue that this this is important because we are meant to get to this as our target this is our expression that we want some x times λ over d and we have already have λ over d so we know that this expression is going to be useful. Then we use regular trigonometry, which says that tangent of this angle is this opposite side divided by the adjacent side so that's y over x and we can solve for y by multiplying both sides by x and then switch the sides around and we have y equals xtan Θ. So Δy is the difference between two consecutive values for y and they are consecutive when one is the y value at an order m plus 1 minus the order before it which is just m and the expression for the y value when you have m plus 1 is x times tan Θ when it's the mth order plus 1 minus x times tan Θ at the mth order and then factor out the x here. Now tan can be replaced with sin of its argument divided by cos of that argument— that's a trigonometric identity— so that's all I have done there. And then we use an approximation because of the small angle so cos of Θ when Θ is really small is approximately the number 1 because the cos graph has a maximum of 1 at Θ equals 0 so the y value here is 1 and this is the Θ axis here and this is zero and if you zoom in on this peak here and consider only values of Θ that are really close to this peak then it's going to be approximately 1 for the y value. Okay so cos of a small angle is approximately 1. So we can substitute this as the number 1 and this as the number 1 as well and then we can make a substitution for sin Θ m+1 using this expression here. So sin of some angle equals the order times the wavelength divided by the slit separation d and I have m+1 in this case and then just m in this case and then multiply the λ by the m and by the 1 and we have λ times m over d plus λ times 1 over d minus mλ over d and these two terms make zero leaving us with x times λ over d and that is Δy and that was what we were meant to show.