Question
An opal such as that shown in Figure 27.17 acts like a reflection grating with rows separated by about . If the opal is illuminated normally, (a) at what angle will red light be seen and (b) at what angle will blue light be seen?

Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 32 (Problems & Exercises)
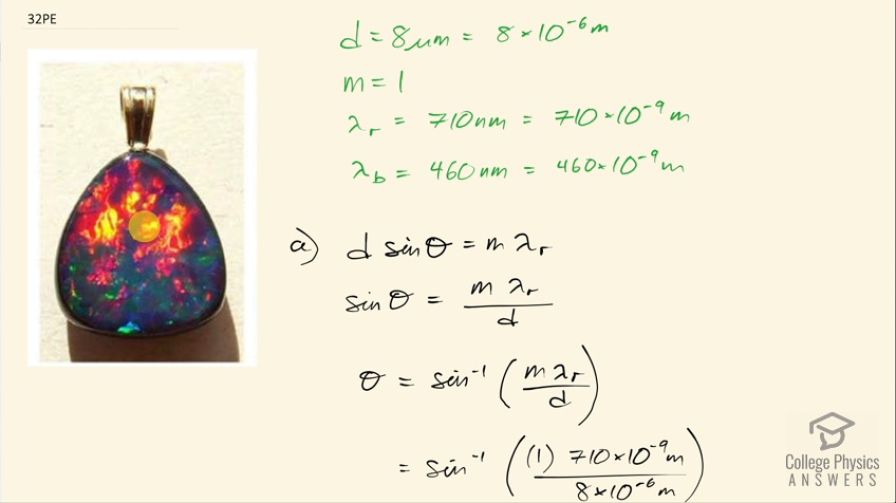
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
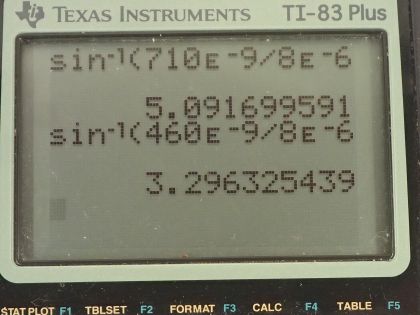
This is College Physics Answers with Shaun Dychko. This piece of opal acts as a reflection grating and the spacing between the features that cause this effect is 8 micrometers, which is 8 times 10 to the minus 6 meters. The first order maximum will be seen at some angle that we want to find out and we want to do it for red light and for blue light so what is the very first maximum you will see for red and the very first maximum you will see for blue? So we need to assign wavelength to these colors and there's some room for interpretation here I am going to say that the red color is 710 nanometers, which is 710 times 10 to the minus 9 meters and blue we'll say is 460 times 10 to the minus 9 meters. So we'll use this formula to find the angle to the maximum we divide both sides by the spacing between the lines and the reflection grating and then we have sin Θ is the order times the wavelength divided by the spacing between lines and then take the inverse sin of both sides and we get then the angle is the inverse sin of the order times the wavelength divided by the spacing. So that's the inverse sin of 1 times 710 times 10 to the minus 9 meters divided by 8 times 10 to the minus 6 meters and that is 5 degrees and I have only one significant figure here just because the spacing between lines in the opal is one significant figure. Now for the blue light, it's the same exact formula but I'll just plug in 460 instead of 710 otherwise the numbers are the same and we end up with an angle of 3 degrees to the first maximum of blue light.