Question
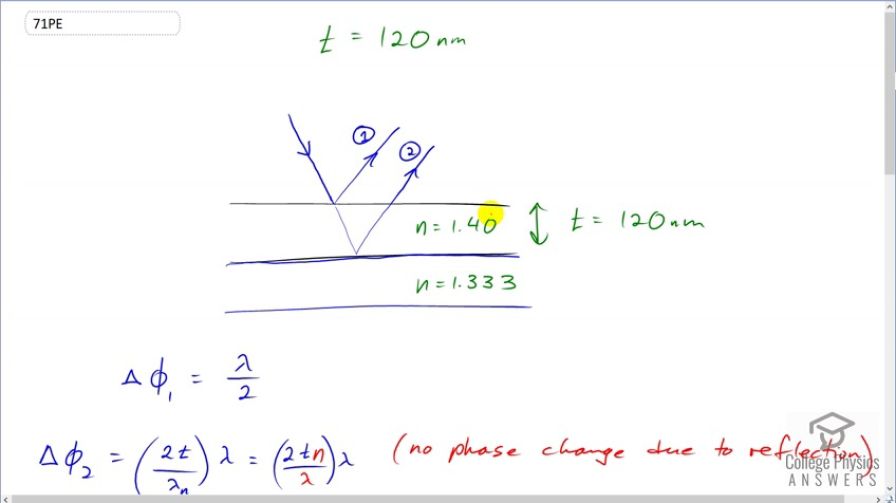
An oil slick on water is 120 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength), given its index of refraction is 1.40?
Final Answer
This is the color red.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 71 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An oil slick is on top of some water and the oil has a thickness of 120 nanometers we're told. It has an index of refraction of 1.4 and it's on top of water which has an index refraction of 1.3. The light ray of white light which means it consists of all the different colors mixed together comes in perpendicular to the oil slick but I've drawn it on an angle just so we can see the two reflected rays. And then I can distinguish between them in the drawing. If I were to draw it straight down then I'd have line straight down and another line straight up and they would all overlap. That would be confusing looking. So we imagine that these rays are actually coming straight down and then reflecting straight back up and mixing together. Now we need to know what is the phase change for each of these reflected rays here and the phase changes measured in number of wavelengths. So it's travelling through air initially which has an index refraction of one and when this ray number one bounces off the top of the oil surface it will have a phase change of half of a wavelength. And that's because it's going from a low index of 1.0 to a material of high index of 1.4 . And so reflecting off of an interface from low to high, causes a phase change of half a wavelength. And then we have to figure out what is the phase shift of this second Ray number two. Now when there's a reflection off of this interface there will be no phase change due to reflection because it's starting. In this material with an index refraction of 1.4 and bouncing off an interface with a material that has a lower index of refraction it's going from a high index and reflecting off of interface with a low index material produces no phase change as a result of that reflection. So we do not have a lambda over two term here. This, by the way, is the way I write phase change with this symbol Phi. And this is Phi 1 which is the phase change of ray one. So the phase change for Ray two is going to be just due to the additional path length of this ray through the thickness of the oil once and then twice. And how many wavelengths will it be shifted. Well it's going to be it's going through the thickness twice and so it's going to be travelling two times a thickness and we're going to divide that by the wavelength but I have a subscript n here because it's the wavelength in this oil material that we're concerned with. So how many wavelengths is this total thickness of 2t, this total path length additional and so that's 2t divided by the wavelength in the material. So the wavelength in the material is the wavelength in an air or a vacuum divided by the index of refraction of the material. And since we're dividing by this we're going to multiply by it's reciprocal. So we're multiplying by n over lambda so we have the phase change for Ray two is two times the thickness of the oil times Index of refraction of oil divided by the wavelength in air times the wavelength in air and these cancel giving us a phase shift of two times index refraction of the oil times the thickness. So constructive interference occurs when you have the total phase shift is some integer multiplied by the wavelength and so we can add these two phase shifts together. And by the way the question asks us what color will the oil b. Well it'll be whatever color constructively interference because constructive interference increases the amplitude of that particular wavelength and it will be the one that is more noticeable. So the total phase shift is gonna be the sum of the phase shifts from each of these rays one and two. And that has to equal m lambda for constructive interference. And then we substitute for each of these. So that's lambda over two phase shift from the reflection at the top of the oil plus two times index of refraction of oil times oil thickness, phase shift for the second Ray that bounces off the oil water interface. And that equals m lambda and then we get rid of fractions because fractions are a bit messy looking and we multiply everything by two and we get lambda plus 4nt equals to m lambda . And then subtract lambda from both sides and we get and then factor out the lambda as well on this right side now and then switch sides around. So we have lambda times bracket 2m minus one equals 4nt and then divide both sides by 2m minus one and so here is the wavelength that will experience constructive interference. It's 4nt over 2m minus one and because this number m is an integer that we can choose. You'll notice that there are many wavelengths that will have constructive interference but the one we're concerned with is the one that is visible. And so we're going to try different values of m . Let's try one first of all. So we have four times index of refraction of oil 1.4 times the thickness of the oil slick 120 nanometres divided by two times m or to choosing to be one minus one which gives 672 nanometres and that is a lucky guess of m equals one because this is visible and this is the color red.
