Question
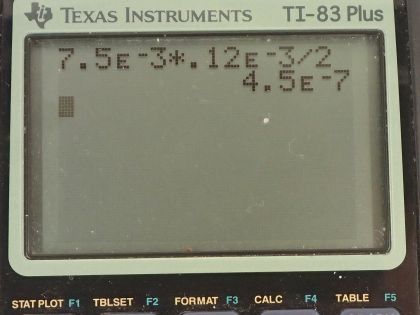
Using the result of the problem two problems prior, find the wavelength of light that produces fringes 7.50 mm apart on a screen 2.00 m from double slits separated by 0.120 mm (see Figure 27.56).
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
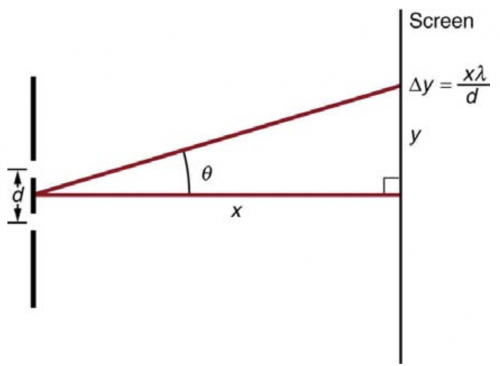
This is College Physics Answers with Shaun Dychko. We have a screen that is a distance x from two slits that are separated by a distance d and we are told that consecutive or adjacent fringes are a distance Δy apart from each other, which is x times the wavelength of the light divided by the separation between the slits and we are told that adjacent fringes are 7.50 millimeters apart and that is 7.50 times 10 to the minus 3 meters the screen is 2.00 meters from the double slit and then the distance between the slits is 0.120 millimeters, which is 0.120 times 10 to the minus 3 meters. So we are going to figure out what is the wavelength of light that produces consecutive fringes that are separated by this much given a screen this far from a double slit where the slits are separated by that much. Okay and this is the formula that does that and we need to rearrange it to solve for λ so multiply both sides by d over x. So the wavelength then is the distance between adjacent fringes times the separation between the slits divided by the distance from the screen to the slits. So that's 7.50 times 10 to the minus 3 meters times 0.120 times 10 to the minus 3 meters divided by 2.00 meters and that is 450 nanometers. I could have left the answer written as 4.50 times 10 to the minus 7 meters but it's tradition kind of in questions involving visible light to express answers in nanometers.