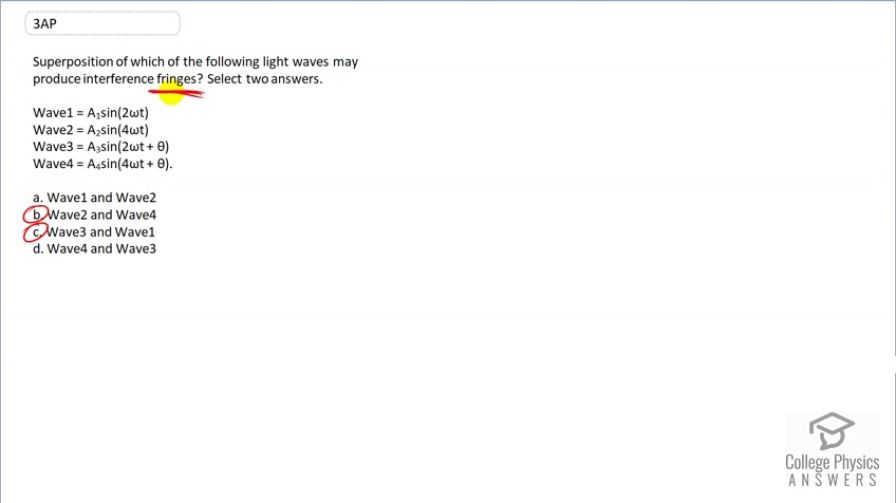
Question
Superposition of which of the following light waves may produce interference fringes? Select two answers.
- Wave1 =
- Wave2 =
- Wave3 =
- Wave4 =
- Wave1 and Wave2
- Wave2 and Wave4
- Wave3 and Wave1
- Wave4 and Wave3
Final Answer
(b) & (c)
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 3 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. In order for two waves to interfere and have destructive interference to create a dark fringe or constructive interference to produce a bright fringe. It's not really clear whether they want dark or bright here, but it doesn't matter. Interference is just the same. The two waves have to have the same frequency or the same wavelength but just be out of phase. And so, wave one and wave three have the same frequency or the same wavelength, whichever way you want to look at it, because the factor in front of T is the same. And, they just differ by this phase difference Theta, assuming Theta is not zero, of course. So, waves one and three can have interference and waves two and four both have a factor four Omega in front of the T, so they have the same frequency and they differ only by this phase shift. And so, waves two and four also can have interference. So, the answer is B and C.