OpenStax College Physics for AP® Courses, Chapter 27, Problem 6 (Test Prep for AP® Courses)

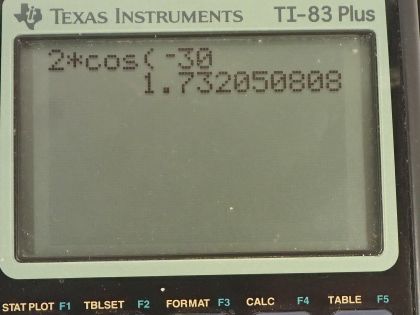
This is College Physics Answers with Shaun Dychko. We consider two waves each with amplitude x and the same phase and the same frequency being added together and the question is what amplitude will the resultant wave have? So xcos Θ plus xcos Θ is 2xcos Θ and it's this factor in front of the cos Θ that is the amplitude so the amplitude is 2x. The question also asks us to graph this picture. So we have in this column A, we have all these angles starting from negative 180 all the way up to 400 and then here we have the formula 2—I had to pick a number for the coefficient of the cos function... we need to pick a number for the amplitude to graph it so I picked the number 2— so x is 2 2 times cos of the angle has to be in radians for this spreadsheet function that's why I am multiplying by π over 180 to convert these degrees into radians. So we have 2 times cos of negative 180 here and then the same in this column and then we add those two together to get this column here and this is the graph of these three different columns and in blue triangles, which are a little bit hard to see because they are obscured by the red x's; that's this curve here which consists of both of these columns being plotted in the same place because they are both the same numbers. Now when you add them together, you get this column here which is the yellow line and it has an amplitude of 4 you can see the peak here is at 4. So this horizontal axis is the angle axis in degrees and then the vertical axis is just the value of the functions. Okay! Then we consider adding... the two waves together that are identical in every respect except for their phase. So now one wave is 60 degrees at a phase with the other so it's translated by 60 degrees horizontally in other words; the amplitude is the same and their frequency is the same. So we are going to first graph the sum of these two waves and see what that looks like and then we are going to calculate the amplitude of the sum. So this column here is a graph of cos Θ and then this column here is cos Θ plus 60 degrees and then this column D is the sum of those two so it's B 2 plus C 2 is the formula and then B 3 plus C 3 and so on and here's a graph of what that looks like. So the cos Θ function is column B, which is in blue— it's this curve here— and then we have cos Θ plus 60, which is translated 60 degrees to the left— that's in red— and then the sum of these two is shown in yellow— it's quite a pretty picture. So we have a peak here it's a little bit... well, this says it's about 3.46 or so so we are going to derive an expression for what this sum is for the amplitude. So our goal in trying to add these together is to come up with an expression that has some number multiplied by cosine of some stuff here and if we can put it in this form then we can say the amplitude is A. So we can factor out the x here and we have x times cos Θ plus cos of Θ plus 60 and we are going to use an identity which is this sum identity for cos of two different arguments— we have cos A plus cos B— and that is 2 times cos of A plus B over 2 times cos A minus B over 2. So A is like Θ and B is Θ plus 60. So we have x times 2 times cos of A plus B so that's Θ plus Θ plus 60 over 2 and then cos of A, which is Θ minus Θ plus 60 all over 2 and this is going to be 2 times x times cos of Θ plus 30 because this is 2Θ up here and 2Θ plus 60 each divided by 2 makes Θ plus 30 times cos of negative 30 so the Θ minus Θ makes zero there and then it's a negative 60 divided by 2 is negative 3. So we have cos negative 30 times 2, which is 1.732 times x times cos of Θ plus 30 so this is the amplitude. So the resultant amplitude is 1.732x.