Question
Prove that, if is the intensity of light transmitted by two polarizing filters with axes at an angle and is the intensity when the axes are at an angle , then
, the original intensity. (Hint: Use the trigonometric identities and
.)
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 90 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
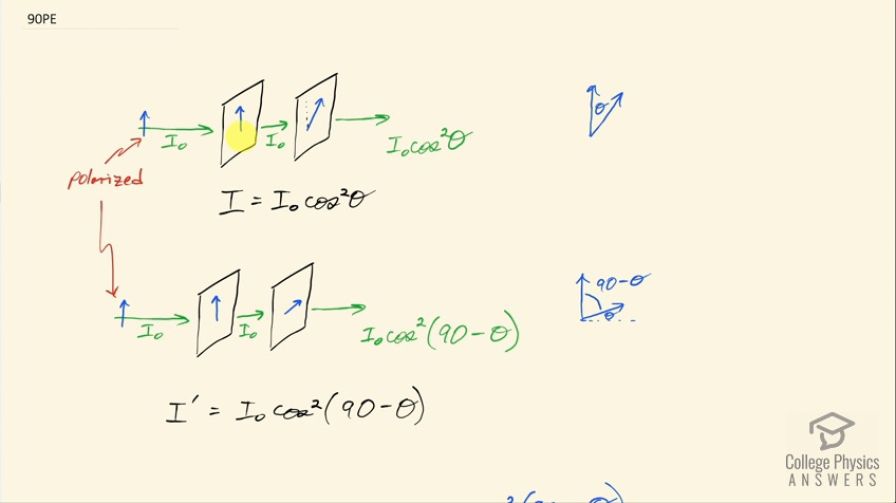
This is College Physics Answers with Shaun Dychko. We have some light traveling through two polarizing films and these films have their axis of polarization at an angle of Θ with respect to each other; we have to assume that the incident light is also polarized and it has its polarization direction aligned with the axis of polarization of the first film so that when it passes through this film, it still has this intensity I naught that it had at the beginning here. So after it passes through the second film, its intensity will be I naught times cos Θ squared and so we are told to label this with the letter I. And then a different arrangement has the axis of these polarizing films aligned at 90 minus Θ with respect to each other. So as originally it was Θ, now we have this angle being 90 minus Θ so that leaves this little portion Θ in here and this is 90 and then this portion is left over 90 minus Θ. Okay! So the intensity after passing through both filters then will be I naught times cos squared of 90 minus Θ and we are told to label that I prime and what we want to show is that I plus I prime equals I naught and we'll get there first by saying, you know, I is I naught times cos squared Θ and then add to that I prime, which is I naught cos squared 90 minus Θ. We have a trigonometric identity, which says that cosine of 90 minus Θ is the same as sin of Θ so we'll replace cos 90 minus Θ with sin Θ of course it's squared and so you know for some reason in trigonometry, they have a funny way of writing squares... it's the same as having it outside here if you were to wrap the whole thing in brackets and put the square out there that would mean the same thing so what we are doing is just replacing this portion inside the square with sin Θ and so you could write it this way as well. Okay! But for some reason in trig, you have the square goes just right beside the letter "n" here or beside the "s." Okay! So we have done that replacement and we can now factor out I naught and so we have I naught times cos squared Θ minus sin squared Θ and there's a trigonometric identity for that which says it equals the number 1— it's called the Pythagorean identity— and so this is I naught and so we have shown that I plus I prime equals I naught.