Question
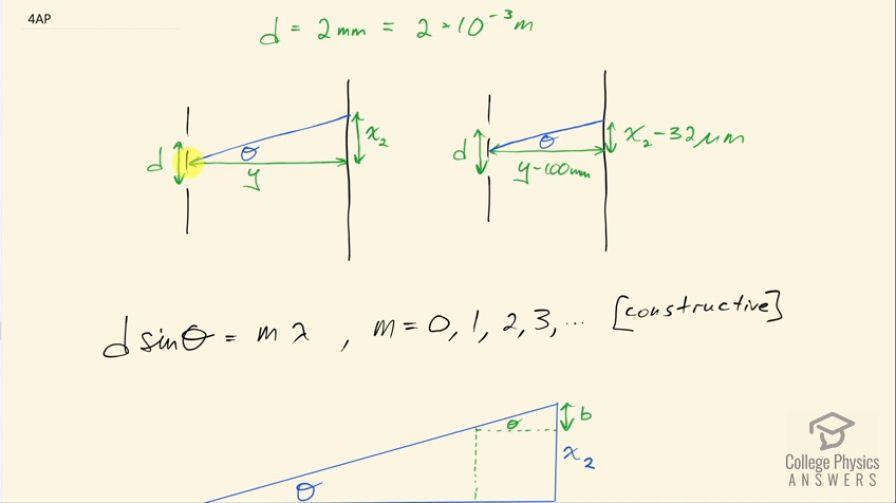
In a double slit experiment with monochromatic light, the separation between the slits is 2 mm. If the screen is moved by 100 mm toward the slits, the distance between the central bright line and the second bright line changes by 32 μm. Calculate the wavelength of the light used for the experiment.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 4 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a double slit experiment where some monochromatic light is being shone on these two slits and there's an interference pattern on this screen and when the screen is moved 100 millimeters closer to the slits, we are told that the second bright fringe is 32 micrometers closer to the central maximum and when it says second bright fringe, I am going to take that to mean the second order constructive interference fringe so we'll have the central maximum here where this is you know the intensity of the light here and then there's a first order maximum here and then the second order maximum here is the second bright fringe they are referring to so m equals 2 in this formula, in other words. Okay! So we have the distance between the slits times sin of the angle to this maximum equals m, which is the order of the maximum times the wavelength λ. Now I have redrawn this triangle here where you have the horizontal distance between the slits and the screen is y and this vertical distance to the second bright fringe is x 2—that's drawn in blue— and then I have also drawn this second picture on top of this blue triangle by saying suppose you move this screen, which was originally here, and you move it to this position 100 millimeters closer—I am calling that the letter a so a is this amount that you move this screen closer and in that case this position of the bright fringe will move down so that's it's here, which is this distance b downwards and we are told that that's 32 micrometers. So this creates a little triangle here— that I have highlighted in yellow— and that triangle we can figure out its angle here and this angle is the same as the angle of the blue triangle because these two triangles are both right triangles and this angle here is shared by both of the triangles so that means this third angle here must be equal so they are both Θ. So we can find Θ for this triangle that's highlighted in yellow, which I have also drawn in green down here and we know that sin Θ is this opposite b divided by the hypotenuse the square root of a squared plus b squared and that sin Θ is something that will go into this formula here for the constructive interference fringes and we can solve this for λ by dividing both sides by m and the wavelength then is d times sin Θ over m and we are going to replace sin Θ with all of this that is b over square root of a squared plus b squared. So d is the distance between the slits and that's 2 millimeters written as 2 times 10 to the minus 3 meters then times that by the distance that the second bright fringe moves down, which is 32 times 10 to the minus 6 meters and divide that by the order of the maximum, which is 2 times square root of 100 times 10 to the minus 3 meters— that's the distance by which the screen has moved closer to the slits— and we square that plus 32 times 10 to the minus 6 meters squared this all works out to 320 nanometers. This is an ultraviolet wavelength and it makes me wonder if the question meant to instead have m equal to 1 by saying that the second bright spot is actually this one here but you know, if we follow the example that's in the textbook... there's an example where it says, you know, the second bright fringe is such and such and it's taking that to mean the order is 2 so we are going to take the order to be 2 here and maybe there's a screen that glows with ultraviolet light, you know, like a... when you have a black light, you can make certain things glow you could have a screen that glows when ultraviolet light hits it in which case you could still see this wavelength indirectly by way of it making the screen glow.
