Question
(a) Find the angle between the first minima for the two sodium vapor lines, which have wavelengths of 589.1 and 589.6 nm, when they fall upon a single slit of width . (b) What is the distance between these minima if the diffraction pattern falls on a screen 1.00 m from the slit? (c) Discuss the ease or difficulty of measuring such a distance.
Final Answer
- This distance would be difficult to measure with the unaided eye, but easily measured using a magnifying glass.
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 51 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
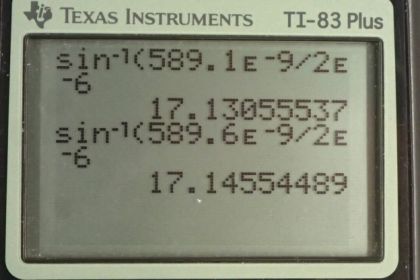
This is College Physics Answers with Shaun Dychko. This question asks us to find the angle to the first minima for these two different wavelengths. 589.1 nanometers and 589.6 nanometers. The slit width through which this light is going to be projected is two micrometers and we have this formula for telling us where the minima are in the diffraction pattern where m is the order or the first or the second or the third minimum. So we'll divide both sides by capital D, the slit width, and then take the inverse sine of both sides and we get the angle then it's the inverse sine of the order times a wavelength divided by the slit width. So the angle to the first order minimum for wavelength a. And so I have my subscripts giving the wavelength label first is this letter a or b, and then the number following it is the, which minimum we're talking about, this is the first minimum. So the angle to the first minimum for wavelength a is the inverse sine of one times 589.1 times ten to the minus nine meters divided by the slit width written as two times ten to the minus six meters giving an angle of 17.130555 degrees. And we're going to keep lots of digits here because we're going to be taking the difference between these two numbers which are different only two very small digits here. So the first minimum for angle or for wavelength b has an angle of inverse sine of the one times this 589.6 nanometers divided by the slit width, giving 17.145545 degrees and so question a ask us to find the difference in the angle to these first two minima. And that's going to be theta b1 minus theta a1 and that works out to 0.0150 degrees. Now for a screen placed one meter away we're asked to figure out what will be the distance between these two minima measured vertically on the screen. So we have this angle for wavelength a, Theta a1 is this angle in here, and then for theta b1 the angle to the first minimum for wavelength b is this in blue here and they will each have some distance from this central maximum here we'll call it y a1, the distance from the center for wavelength a to the first minimum. And then y b1is up here and then the difference between those two is gonna be the answer to our question. Delta y being the distance between the minima on the screen. Now we're going to use tangent and tangent theta is gonna be the opposite over the adjacent and so we have this right triangle here for wavelength a and the opposite will be the y and the adjacent is going to be the x. And so to solve for y we're gonna multiply both side by x here and so y is x times Tan theta. So for y wavelength b first minimum we're going to substitute x times Tan theta b1 and then minus from that substitution for y a1 with x Tan Theta a1 and then the x can be factored out. And so we have x times the difference in the tangents of the two angles. So that's going to be one meter times Tan of 17.145545 degrees minus Tangent of 17.130555 degrees, giving 287 micrometers is the distance between these two minima here. And this distance would be difficult to measure with your naked eye but it would be easily measured if you had a magnifying glass.