Question
A film of soapy water ( n = 1.33 ) on top of a plastic cutting board has a thickness of 233 nm. What color is most strongly reflected if it is illuminated perpendicular to its surface?
Final Answer
(orange)
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 74 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
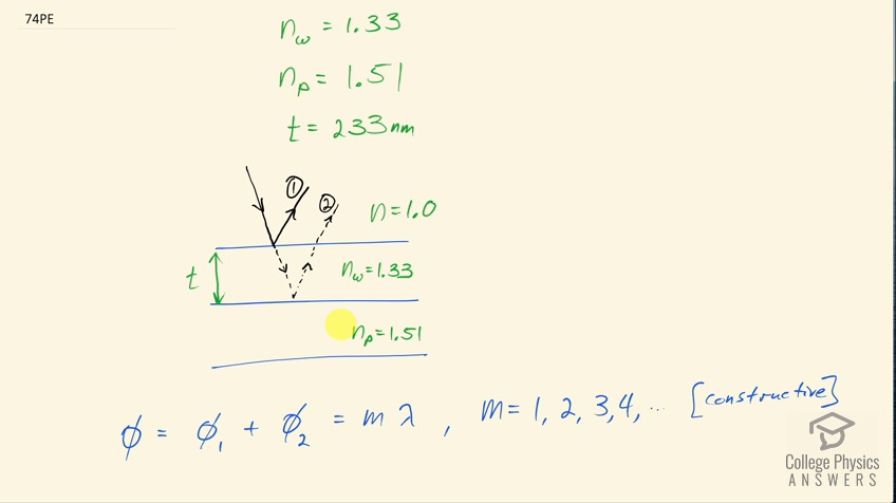
This is College Physics Answers with Shaun Dychko. A 233 nanometer thick film of soapy water is on top of a plastic cutting board and some white light is incident on the soapy film and it's coming in at an angle that's 90 degrees and then there are two reflections happening that are important here: one is from the initial interface between the air and soapy water and then there's a second reflection that happens off of this interface between the water and the plastic cutting board. Now in reality, the light is coming straight down and these reflections are coming straight back up and this will all overlap and get messy in our drawing and so I am drawing the light coming in at an angle in order to distinguish between these two reflections— one from the top interface and one from this bottom interface— so we have ray one and ray two. There's a phase shift for each of these rays the reflection that happens here is a phase shift of half of a wavelength automatically because the ray is traveling from a low index of refraction of air, which is 1.0 and then reflecting off an interface where the second medium has a higher index of refraction and that's 1.33 we are told and so there's going to be a phase shift of λ over 2 and so our phase shift is measured in number of wavelengths and so we have half of a wavelength phase shift for ray one. Ray two is going to have a phase shift due to reflection here because it's going from low index—1.33— and then the second index of refraction I am assuming is about 1.51 it's not really clear what it should be but plexi-glass is kind of like plastic so I am going to take 1.51 to be the index of refraction of the plastic cutting board and so there is a λ over 2 or half wavelength phase shift due to this reflection here and so the total phase shift for the second ray is going to be λ over 2 plus the phase shift due to this increased distance that the ray is traveling. So the number of wavelengths that this number represents is 2 times the thickness of this film because it's traveling this thickness twice— once down and then again on the return— so 2 times the thickness divided by the wavelength but it's the wavelength that's in the film that matters here and then we multiply that by the wavelength in the air so this fraction is the number of wavelengths of phase shift and then we turn it into units of wavelengths by multiplying it by the wavelength in air. Okay! So... this λ n is the wavelength in air divided by the index of refraction of the water and so we replace λ n with λ over n but since we are dividing this fraction by this fraction, I am instead going to multiply by the reciprocal of this fraction so we have n over λ here. The λ's cancel and we are left with our phase shift for the second ray is λ over 2 plus 2 times the thickness times the index of refraction of the water or the soapy water. So the total phase shift is going to be the sum of these phase shifts of rays one and two and it has to equal some natural number times the wavelength in air in order to have constructive interference. So we have λ over 2 plus λ over 2 plus 2tn equals mλ and we can collect these two together— λ over 2 plus λ over 2 is λ— and then subtract λ from both sides and we get this here mλ minus λ and that equals 2tn and factor out the λ and we have m minus 1 times λ equals 2tn. We want to solve for the wavelength and so we are dividing both sides by m minus 1 because we want to know which color is most strongly reflected or which color has the greatest constructive interference in other words. So we have λ is 2 times the thickness times the index of refraction of the soapy water divided by m minus 1. Now we can't take m equal to 1 because that would make this fraction undefined when we divide it by zero so we'll take m equal to 2 and so λ then is 2 times the soapy water thickness, which is 233 nanometers times the index of refraction of the soapy water—1.33— divided by 1 and this is 619 nanometers, which is the color orange.
