Question
Calculate the wavelength of light that has its third minimum at an angle of when falling on double slits separated by . Explicitly, show how you follow the steps in Problem-Solving Strategies for Wave Optics.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
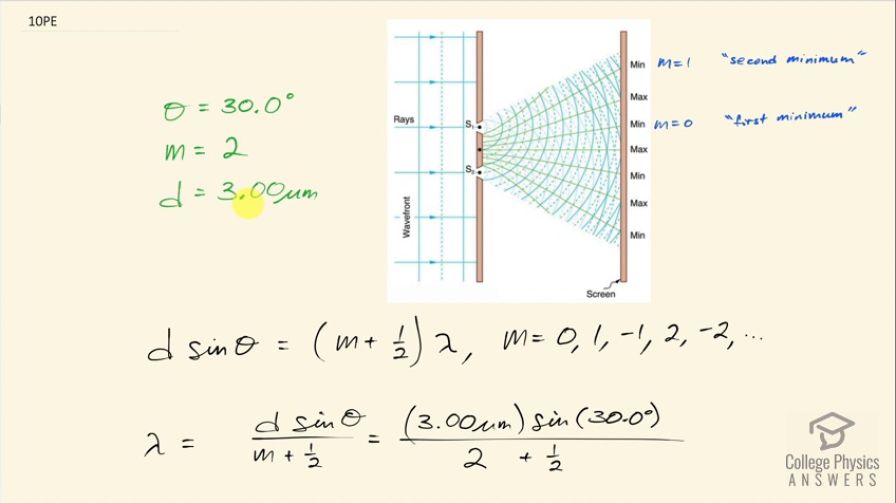
This is College Physics Answers with Shaun Dychko. We need to calculate the wavelength of light that is incident on two slits that are separated by 3.00 micrometers given that the angle to the third minimum is 30.0 degrees. Now when you have the third minimum, the order is actually 1 less than that so in this picture here we can see that there's the first minimum occurring here on either side of the central maximum and that is corresponding to order zero and we have the second minimum here which is m equals 1. So in this formula the order is 1 less than you know the occurrence of it so the first occurrence is m 0 and the second occurrence is m 1 and the third occurrence is m 2. Okay! So here's a formula for destructive interference in the double-slit experiment so we have the separation between slits d times sin Θ—the angle to the minimum— equals the order plus a half times the wavelength of light and we'll divide both sides by m plus a half to solve for the wavelength λ. So the wavelength then is 3.00 micrometers— separation between slits— times sin 30.0 degrees divided by the order of 2 plus a half and that works out to 0.600 micrometers and times that by a 1000 nanometers per micrometer and that is 600 nanometers, which I write as 6.00 times 10 to the 2 nanometers in order to be explicit about the number of significant figures.
