Question
What is the ratio of thicknesses of crown glass and water that would contain the same number of wavelengths of light?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 5 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
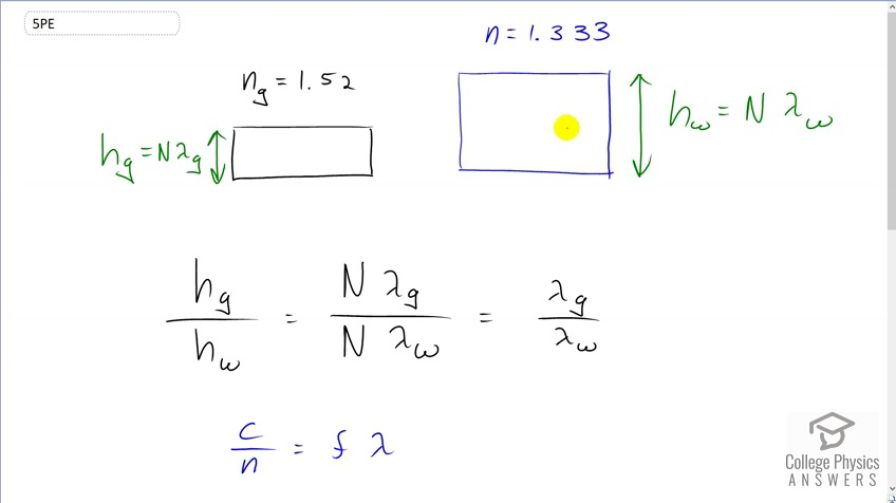
This is College Physics Answers with Shaun Dychko. We have some thickness of crowned glass which has an index of refraction of 1.52 and a different thickness of water with an index of refraction of 1.33. And, the height are such that they both contain the same number of wavelengths. And so, the height, in terms of the wavelength, is going to be the number of wavelengths times the number of nanometers per wavelength. And, this capital N is the number of wavelengths and it does not have a subscript because we're told that the number of wavelengths should be the same in the water as in the glass. So, we can divide these two heights to find their ratio and then substitute capital N times the wavelength in the glass divided by capital N times the wavelength in the water. And then, the N's cancel and then we're left with the ratio of heights as the same as their ratio of their wavelengths. Now, we don't know what their wavelengths are, but we do know their indexes of refraction of these two materials. And so, we'll use that. We'll have to express wavelength in terms of index of refraction. And then, we'll be able to substitute into here to get the answer. So, we know that the speed of a light wave is the speed of light in a vacuum divided by the index of refraction, and that is the frequency times the wavelength in the medium. Usually, this has a subscript N here on the wavelength to indicate that it's the wavelength in some medium, not in a vacuum. So, we can solve for Lambda by dividing both sides by frequency. And then, we see that the wavelength in glass as the speed of light in a vacuum divided by the index of refraction of the glass times frequency. And, the wavelength in water is the speed of light in a vacuum divided by the index of refraction of water times frequency. The frequency does not get a subscript G or W here because the frequency is the same. It's only the wavelength that changes as light passes between media. So, when we have this ratio of the heights, then, we're going to substitute these expressions in place of the wavelengths. So, for wavelength of glass, we have C over N G F and then we're dividing by the wavelength in water, which is the same as multiplying by its reciprocal. And so, I'm going to multiply by Nw F over C and then a whole bunch of things cancel, leaving us with index of refraction of water divided by index of refraction of glass. So, the thickness of the glass divided by thickness of water is going to be 1.333 divided by 1.52, which is 0.877. So, the height of this glass, in order to have the same number of wavelengths as in water, the height of the glass will be 0.877 times the height of the water, and so it will be smaller.
