Question
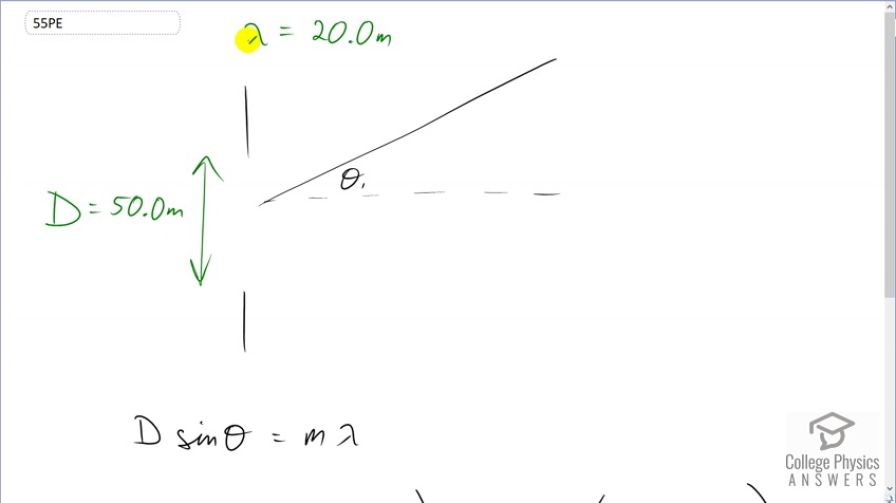
A water break at the entrance to a harbor consists of a rock barrier with a 50.0-m-wide opening. Ocean waves of 20.0-m wavelength approach the opening straight on. At what angle to the incident direction are the boats inside the harbor most protected against wave action?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 55 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. All types of waves experience diffraction in the same way as light waves do and so water waves with a wavelength of 20 meters approaching this gap into a harbor which is 50 meters wide will also experience diffraction. So at this angle theta one this is going to be the angle to a minimum here of the of the water waves when they reach the boats which he suppose are all scattered around here somewhere and the preferable place to put a boat would be here because then the waves would be the smallest there. And you know in a perfect scenario they would be no wave at all at this particular position. So let's figure out what theta one is. So we have this formula for a diffraction pattern and we will solve it for theta by dividing both sides by d the slit width or the size of this opening through which the waves are travelling. And so if theta is going to be the inverse sine of m lambda over D. So the inverse sine of one times 20 meter wavelength divided by 50 meter slit width giving an angle of 23.6 degrees. So if you position your boat here at an angle of 23.6 degrees with respect to this horizontal that is the best place to put the boat where there would be a minimum in the wave.
