Question
(a) Sodium vapor light averaging 589 nm in wavelength falls on a single slit of width . At what angle does it produces its second minimum? (b) What is the highest-order
minimum produced?
Final Answer
- 12
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 49 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
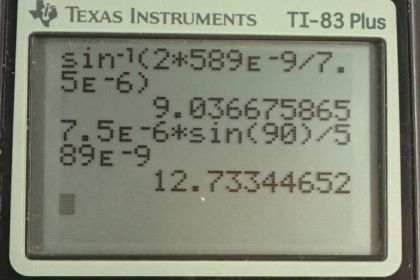
This is College Physics Answers with Shaun Dychko. We begin by writing the information down that we know the wavelength is 589 nanometers and the slit width is 7.5 micrometers in part a we want to know where will the second minimum be. And so the order m is two in this formula. So this is the slit width time sine of the angle to the minimum equals the order times the wavelengths of the light. So we're gonna solve for theta by dividing both sides by d and then taking the inverse sine on both sides. So the inverse sine for the second order minimum is gonna be inverse sine of two times 589 times ten to the minus nine meters divided by 7.5 times ten to minus six meters giving 9.04 degrees is the angle to the second minimum. Part b asks us what will the highest order minimum be in this diffraction pattern? Well the highest order minimum will occur when the angle is at 90 degrees. Now of course not precisely 90 degrees because at that point if we were to draw a picture of the situation we have some slit here and a screen here and light with a wavelength of 589 nanometers which is somewhere between blue and red, let's call it green and it’s minimum is at 90 degrees. Well it's going to be parallel to the screen and it won't actually touch the screen. But 90 is that border between when it just does touch the screen. If it were that 89.9 degrees, say, compared to the central maximum. And so we take 90 to be that border and we solve for and we get 12.73 and this rounds in this case to the number 12. It does not round to 13. We're not doing a mathematical rounding of this number. We're doing a physical rounding. We're considering the physical situation and taking the number that makes sense in this context which is 12 because this means that the minimum is going to be somewhere at an angle of less than 90 and taking 13 would give an angle greater than 90 which is non-physical because it would mean the minimum is over here somewhere and not even on the screen. So the highest order minimum is 12.