Question
What angle is needed between the direction of polarized light and the axis of a polarizing filter to cut its intensity in half?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 27, Problem 84 (Problems & Exercises)
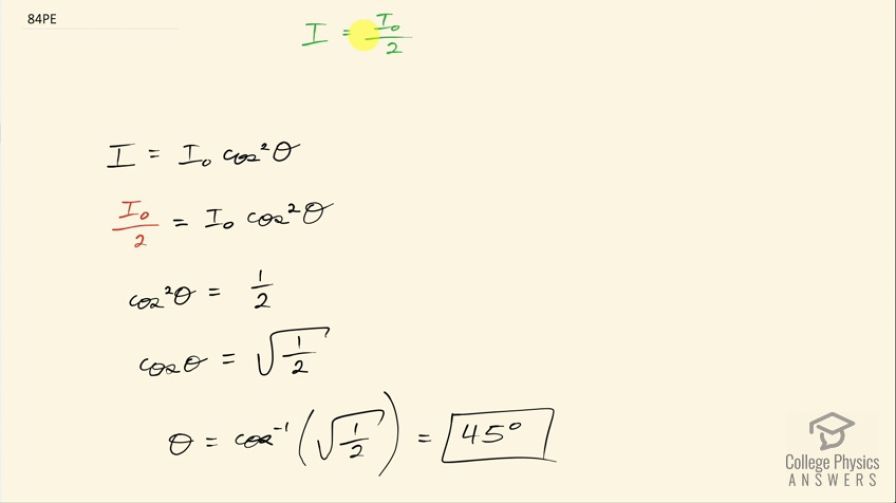
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When polarized light passes through a polarizing filter, we are told that the intensity after passing through it will be half of what it was initially so that means I equals I naught over 2 in this formula here here's the intensity after the polarizing filter here's the intensity before the polarizing filter and we are taking the square of the cosine of the angle between the direction of the polarization of the light and the axis of the polarization filter. Okay! So replace I with I naught over 2 and then divide both sides by I naught or multiply by 1 over I naught and we have this line here where cos squaredΘ equals one-half. So cos squaredΘ—it's a bit of funny way that they write squaring of trig functions, you could instead write it like this and it would mean the same thing— and we want to take the square root of both sides so we get cos Θ then is the square root of a half and then take the inverse cos of both sides to solve for Θ. So the angle then between the axis of the polarizer and the polarization axis of the incident light is the inverse cos of the square root of a half, which is 45 degrees.
