Question
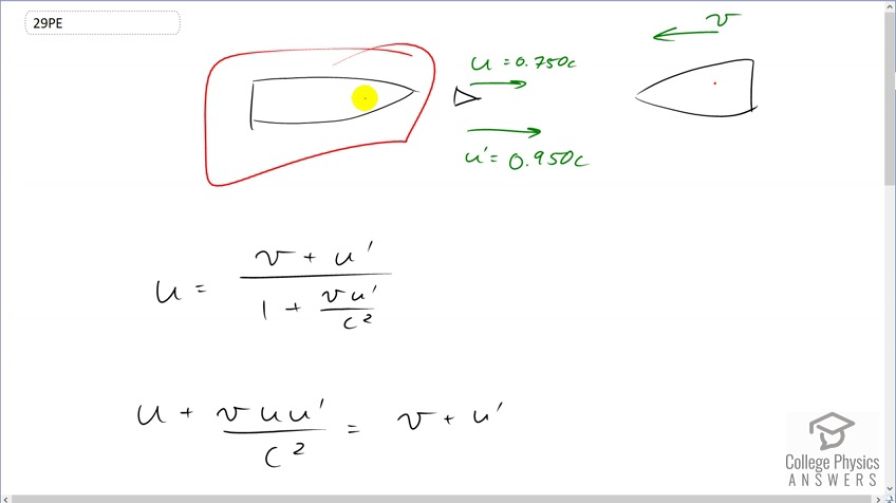
What is the relative velocity of two spaceships if one fires a missile at the other at and the other observes it to approach at ?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 29 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. These two spacecraft are approaching each other and let's assume that this spacecraft, we'll take this spacecraft to be the reference frame that is at rest. In that case, this spacecraft is moving to the left towards it. And this velocity of this bullet is going to be measured by the reference frame that is at rest so we'll call it u and it's 0.750c and that makes this other velocity 0.950c reported by the person in the moving reference frame is u prime. And so our job is to solve for v, the velocity with which this reference frame is moving. So u equals v plus u prime over 1 plus v times u prime over c squared; that's relativistic addition of velocities formula and we need to do a bunch of algebra to solve for v. So we'll begin by multiplying both sides by this bracket, 1 plus v u prime over c squared, and it cancels on the right side and shows up on the left and gets multiplied by u and so that's why we have u plus v u u prime over c squared equals v plus u prime. And then we'll collect the v terms together and so we'll substract v from both sides so it's 0 on the right side and it shows up as minus v on the left and we'll also get rid of this minus u on both sides. So on the left we have v u u prime over c squared minus v equals u prime minus u, on the right side. Then we factor the v out and we have v times bracket u u prime over c squared minus 1 equals u prime minus u and then we can divide both sides by this binomial. And so we have the velocity of the second spacecraft or the moving reference frame, in other words, is u prime minus u over the product of the two velocities— u and u prime divided by c squared minus 1. So that's 0.950c minus 0.750c over 0.750c times 0.950c divided by c squared minus 1, which is c times 0.950 minus 0.750 over the product of 0.750 and 0.950 minus 1, which is negative 0.696c. So this ship is moving to the left because our coordinate system has positive to the right; that other spaceship is moving to the left with a velocity of 0.696c or, in other words, the ships are approaching each other with this velocity.
