OpenStax College Physics, Chapter 28, Problem 56 (Problems & Exercises)

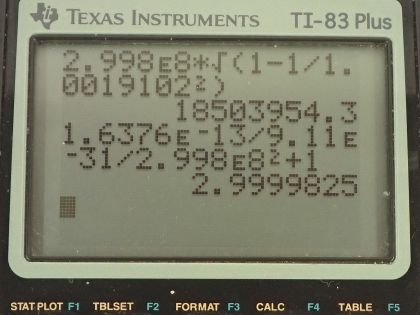
This is College Physics Answers with Shaun Dychko. When a positron and an electron meet, all of their mass is converted into energy and so the total energy that will result from their meeting will be 2 times the rest mass energy of one of them because they each have the same rest mass energy and we assume that there's negligible amounts of kinetic energy before this collision. So that's 2 times the rest mass of an electron times c squared that's 2 times 9.11 times 10 to the minus 31 kilograms times 2.998 times 10 to the 8 meters per second squared and that's 1.64 times 10 to the minus 13 joules. In part (b) we are asked if this energy was given to a proton in the form of kinetic energy, what would its speed be? So kinetic energy is this Lorentz factor γ minus 1 times the rest mass energy of the particle and here we are talking about a proton so we have the rest mass of a proton here with subscript P to indicate that. We have to solve for γ because then once we know γ, we can find the speed because here's another expression for γ in terms of speed of the particle. Okay! We are going to first divide both sides by the rest mass energy or the rest energy of this proton and that is γ minus 1 then is the kinetic energy divided by mass of the proton times c squared then add 1 to both sides and you get γ is kinetic energy divided by m Pc squared plus 1 and then substitute in this kinetic energy which we calculated in part (a) and divide that by the rest mass of a proton—1.67 times 10 to the minus 27 kilograms— times the speed of light squared plus 1 and that's 1.00109102. Then we have this expression for γ is 1 over square root 1 minus v squared over c squared and we have to solve this for v. So first we'll multiply both sides by 1 minus v squared over c squared and divide both sides by γ squared after squaring both sides so I am kind of doing two steps at once here. So square both sides first and then afterwards multiply by this fraction and we'll be left with 1 minus v squared over c squared equals 1 over γ squared and then add v squared over c squared to both sides and subtract 1 over γ squared from both sides and you get v squared over c squared is 1 minus 1 over γ squared. Now multiply both sides by c squared and you get v squared is c squared times 1 minus 1 over γ squared and then square root both sides to solve for v. It's the speed of light times the square root of 1 minus 1 over γ squared. So that's 2.998 times 10 to the 8 meters per second times the square root of 1 minus 1 over 1.00109102 squared that's 1.85 times 10 to the 7 meters per second would be the speed of the proton if the proton had 1.64 times 10 to the minus 13 joules of kinetic energy. Part (c) says suppose this energy is given to an electron. So we are going to repurpose the formulas that we derived in part (b) here; a formula for γ is kinetic energy over the mass times speed of light squared plus 1 and then the mass we will use now is the mass of an electron. So that's the answer for part (a) divided by the rest mass of an electron times the speed of light squared plus 1 and that's 3.0000 and then the speed is the speed of light times the square root of 1 minus 1 over that γ. So that's the speed of light times square root 1 minus 1 over 3.000 squared and this is 2.83 times 10 to the 8 meters per second.