OpenStax College Physics, Chapter 28, Problem 37 (Problems & Exercises)

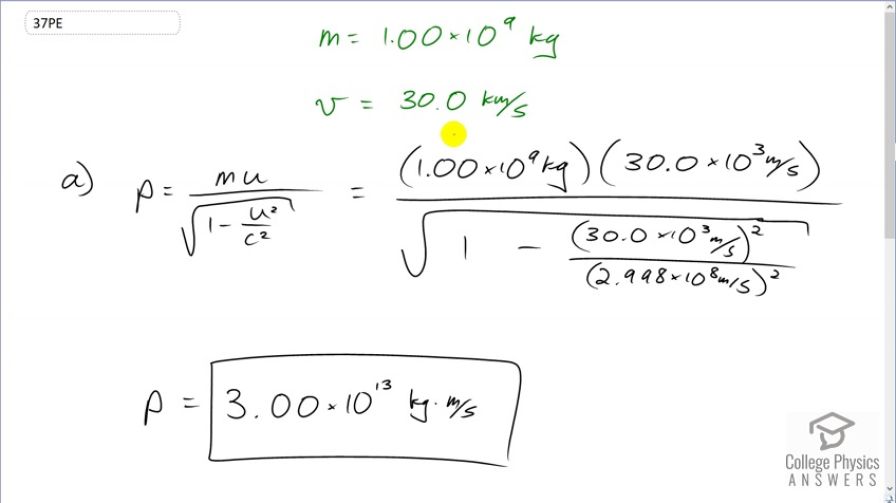
This is College Physics Answers with Shaun Dychko. An asteroid with the mass of 1 times 10 to the 9 kilograms is approaching Earth with a speed of 30 kilometers per second and we want to know its relativistic momentum. So it's gonna be its mass times its approach velocity divided by square root of 1 minus the approach velocity squared divided by c squared. So that's 1 times 10 to the 9 kilograms times 30 times 10 to the 3 meters per second— converting the prefix kilo into times 10 to the 3— and divide by square root 1 minus 30 times 10 to the 3 meters per second squared divided by speed of light squared. This works out to 3.00 times 10 to the 13 kilogram meters per second. This is the actually the answer that we would have expected with a classical calculation, where we would just take the product of mass times velocity, at least to 3 significant figures, it's the same. So we are expecting the ratio in part (b), the relativistic momentum divided by classical momentum, we are expecting this ratio to be pretty close to 1 since we are seeing that to 3 significant figures, there's no difference. And so it's gonna be this Lorentz factor, gamma, times mass times velocity divided by the classical formula, which is just mass times velocity. giving us gamma is the ratio. So we use the binomial approximation for this 1 over square root 1 minus u squared over c squared and that is 1 plus a half u squared over c squared. So that's 1 plus a half 30 times 10 to the 3 meters per second squared and then divide by 2.998 times 10 to the 8 meters per second squared giving 1.000000005 and it's very close to 1, as we expected.