Question
A supernova explosion of a star produces of energy. (a) How many kilograms of mass are converted to energy in the explosion? (b) What is the ratio of mass destroyed to the original mass of the star?
Final Answer
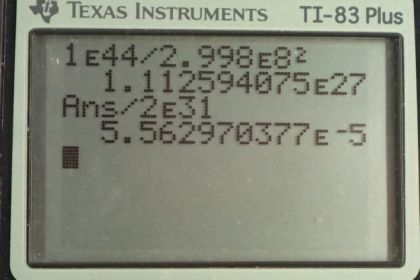
- $1.11 \times 10^{27} \textrm{ kg}
- $5.56 \times 10^{-5}
Solution video
OpenStax College Physics, Chapter 28, Problem 47 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. 1.00 times 10 to the 44 joules of energy is produced by a star explosion. And the initial mass of the star was 2 times 10 to the 31 kilograms. The question is how much mass was converted into energy? So energy equals the amount of mass converted times c squared. And so we can solve for this delta m by dividing by c squared. So delta m is the energy divided by speed of light squared. So that's 1 times 10 to the 44 joules over speed of light squared, which is 1.11 times 10 to the 27 kilograms. Part (b) asks us to find the ratio of mass that was converted into energy. And so we'll take the amount of mass lost— which we calculated in part (a)— and divide that by the initial mass of the star. That gives a ratio of 5.56 times 10 to the minus 5. So very little of the star's initial mass was converted into energy despite the fact that there is such a huge amount of energy produced.