Question
Show that for any relative velocity between two observers, a beam of light projected by one directly away from the other will move away at the speed of light (provided that is less than , of course).
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 33 (Problems & Exercises)
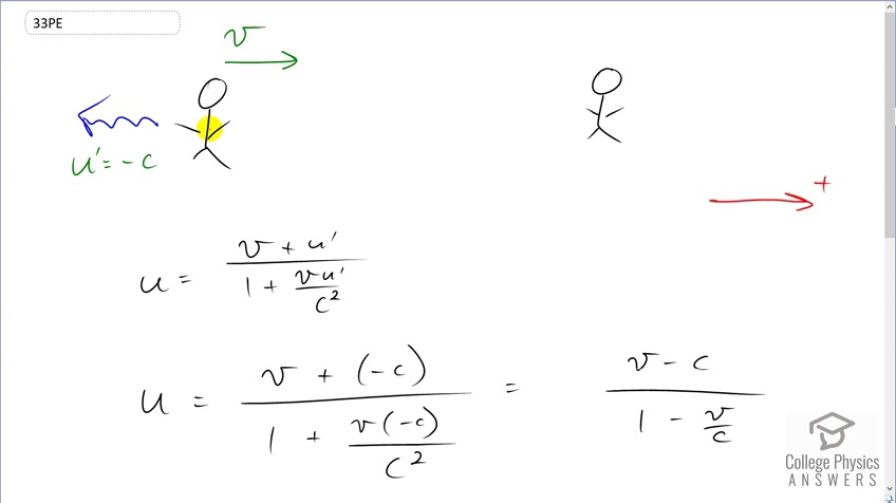
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to choose some relative velocity between two observers and one of the observers emits some light away from the other observer which of course has a speed of c, according to this particular observer. And the speed of this light measured by this moving observer because we have chosen to have this observer on the right, at rest. And we'll say that the observer on the left is the reference frame that is moving with some velocity v. And the speed that this person that is moving observes for the light is going to be labeled u prime. And so we have this relativistic addition of velocities formula which says that the velocity observed by the person at rest is going to be the velocity with which the other observer is moving plus the velocity that they report divided by 1 plus v u prime over c squared. So we are taking the right to be positive and that means this velocity—u prime— is going to be negative c because it's towards the left. And let's see what u observes. So we plug in negative c in place of u prime. So u is v plus negative c over 1 plus v times negative c over c squared. So on the top it's v minus c and on the bottom, we have one of the c's in the bottom canceling with this c at the top and that makes negative v over c. Then we multiply top and bottom by c over c and on the bottom, we have 1 times c is c. And then minus v over c is just going to be v. Then on the top, we have c times v minus c. Then let's multiply this by negative 1 and then multiply the c by negative 1. So we are multiplying by 1, in other words, negative 1 times negative 1 and this bracket when it's multiplied by negative 1 ends up having the signs changed inside so it's c minus v and this negative 1 stays there so negative c. And so we have created binomials that are the same and these cancel. And so we have the u is negative c. And so quod erat demonstrandum, we have shown that the velocity of this light measured by this person is gonna be negative c, just the same as the velocity measured by the moving observer.