Question
(a) How far does the muon in Example 28.1 travel according to the Earth-bound observer? (b) How far does it travel as viewed by an observer moving with it? Base your calculation on its velocity relative to the Earth and the time it lives (proper time). (c) Verify that these two distances are related through length contraction .
Final Answer
- Yes, the Lorentz Factor relates the two distances.
Solution video
OpenStax College Physics, Chapter 28, Problem 14 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
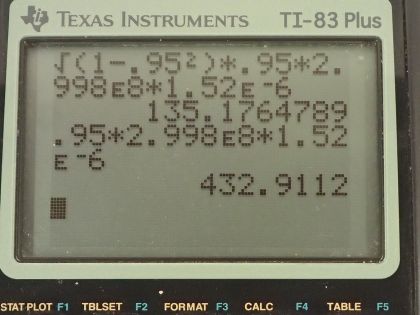
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A muon has a lifetime in its reference frame of 1.52 microseconds so this means if an observer is traveling with the muon, in which case they are not moving at all with respect to the muon because they are going with it, they are measuring proper time and so that's 1.52 microseconds; the speed of a muon is 0.950 times the speed of light and the question in part (a) is how far does the muon travel according to an Earth-based observer? So an Earth-based observer will measure L and that's going to be square root of 1 minus v squared over c squared times the proper length or the proper distance that the muon travels and this is according to the muon observer. the observer moving with the muon will measure L naught and L naught will be the speed of the muon times the proper time measured by this reference frame of the muon. So we can replace L naught with vt naught and then the distance measured on Earth then is going to be the square root of 1 minus 0.950c squared over c squared and that's maybe multiply by 0.950 times the speed of light as a number here— 2.998 times 10 to the 8 meters per second— times 1.52 times 10 to the minus 6 seconds— proper time lifetime— and this works out to 135 meters. Part (b) asks what distance will a muon travel according to an observer moving with the muon? And that's going to be the speed of the muon times proper time. So that's 0.950 times the speed of light times the lifetime of the muon and the muon's reference frame and that's 433 meters. And question (c) is asking are these numbers... these lengths are they related by this Lorentz factor this thing called γ? And that's our formula for the contracted length equals the proper length divided by γ. So that's 432.9112 meters divided by 3.20 and that equals 135 meters and so yes indeed, you can find the contracted length by dividing the proper length by γ to get the length measured in the Earth-bound reference frame.