Question
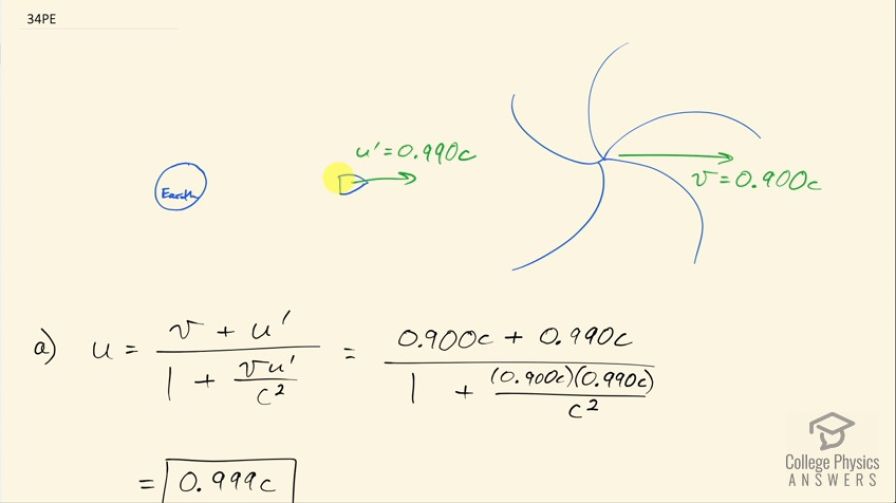
(a) All but the closest galaxies are receding from our own Milky Way Galaxy. If a galaxy away is receding from us at , at what velocity relative to us must we send an exploratory probe to approach the other galaxy at , as measured from that galaxy? (b) How long will it take the probe to reach the other galaxy as measured from the Earth? You may assume that the velocity of the other galaxy remains constant. (c) How long will it then take for a radio signal to be beamed back? (All of this is possible in principle, but not practical.)
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
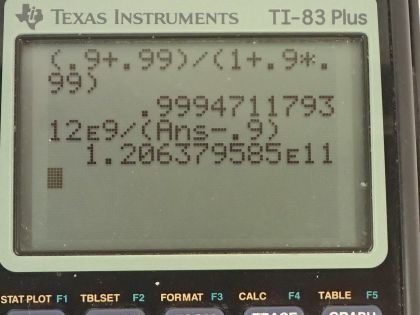
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A galaxy is receding away from Earth with a speed of 0.900c and a space probe was launched from Earth towards the galaxy and the galaxy observer would notice the space probe approaching at 0.990c and the question is what speed would the Earth report for the speed at which this probe is receding from the Earth? So u prime is the label given to this speed reported by the galaxy since the galaxy has been labeled with the velocity v so whatever a person on the reference frame labeled with v reports as the speed for this probe their version will get the label u prime in which case, u, the velocity of the probe measured by an Earth-based observer will be v plus u prime over 1 plus v times u prime over c squared. So that's 0.900c plus 0.990c divided by 1 plus 0.900c times 0.990c over c squared and that is 0.999c. Part (b) says how long will it take the probe to reach the other galaxy as measured from the Earth? So we have this proper distance to the galaxy given to us— it's 12 billion light years— and Earth is at rest with respect to this initial position of the galaxy and that initial position doesn't change. Over time of course the galaxy does move but it's this initial position that we are measuring here so this is L naught and over time, the galaxy moves to the right until finally, it meets this space probe which is moving faster than the galaxy and it meets it at this point labeled x final... x f; here's x equals 0 at the Earth where the probe is initially launched from and we can create an expression for the final x-position for the galaxy and for the probe and the final position is the same for each of them since they both reach the same location. So for the galaxy, it gets a head start— it starts at L naught— and then add to that the speed that the galaxy moves multiplied by this time that we have to figure out— how long does it take to get to this meeting point? And then the space probe will get to that point starting from zero and then it is going to be its velocity as measured by an Earth-based observer times time. So we equate these two expressions and then we are going to solve for Δt: we'll subtract vΔt from both sides and we get this line here and then factor out the Δt and then divide both sides by u minus v and we get the time then is this proper distance divided by u minus v. So that's 12.0 times 10 to the 9 light years divided by 0.99947c minus 0.900c and this denominator becomes some number times c and light years could be abbreviated instead with c y if you like because it really means this speed of light multiplied by a year because it's the distance that light travels, which happens at the speed c times a period of a year and so the c implicit in the light years cancels with the c factor in the denominator and we are left with units of years in our time so that's 1.21 times 10 to the 11 years. Now while this space probe is busy catching up to the galaxy, the galaxy is receding further away from Earth until after the space probe arrives at the galaxy is now at this position x f away from the Earth— it's no longer at L naught that was originally given to us— it's now L naught plus the speed of the galaxy multiplied by the amount of time it took for the space probe to catch up and this total distance divided by c is going to be the time it takes for the light to get from the galaxy back to the Earth— by light I mean the radio signal transmitted by the probe back to Earth. So that's 12.0 times 10 to the 9 light years— original distance between the Earth and the galaxy—plus 0.900c—recession velocity of the galaxy—times this time it takes for the probe to catch up— 1.21 times 10 to the 11 years— and so this becomes has units of speed of light multiplied by years just as the same as this does and then we are dividing all that by c and so this will end up being in units of years. So that will be 1.21 times 10 to the 11 years for the light to get back from the galaxy to Earth, which is significantly longer than the age of the universe and so this is an impractical amount of time.