Question
(a) Beta decay is nuclear decay in which an electron is emitted. If the electron is given 0.750 MeV of kinetic energy, what is its velocity? (b) Comment on how the high velocity is consistent with the kinetic energy as it compares to the rest mass energy of the electron.
Final Answer
- Since the mass of the electron is so small (), the velocity needs to be compensatingly very high.
Solution video
OpenStax College Physics, Chapter 28, Problem 55 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
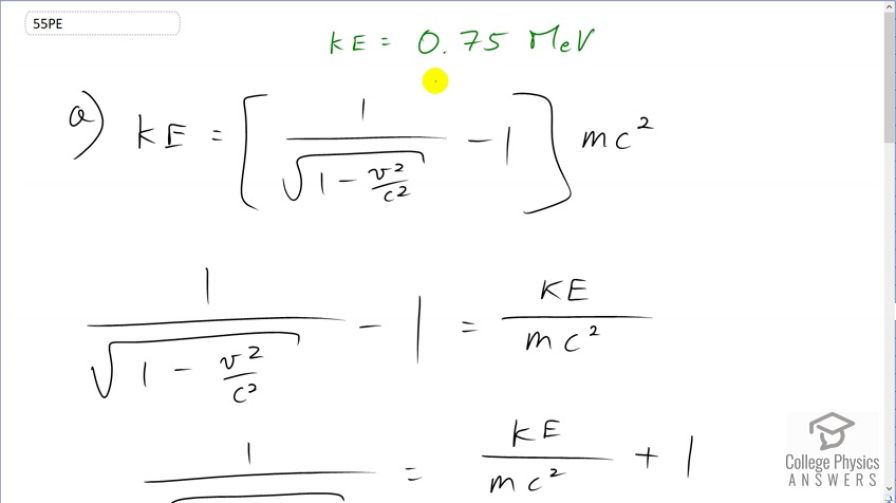
This is College Physics Answers with Shaun Dychko. An electron has a kinetic energy of 0.75 megaelectron volts and this kinetic energy is the Lorentz factor, which is normally written as gamma but we can substitute gamma as 1 over square root 1 minus speed squared over speed of light squared minus 1 times the mass times speed of light squared. Our job here is to solve for v in order to figure out the speed of this electron. So first thing we'll do is divide both sides by mc squared and switch the sides around and we have 1 over square root 1 minus v squared over c squared minus 1 equals kinetic energy over mc squared. And then we'll add 1 to both sides to get this line here and then raise both sides to the exponent negative 1 in order to flip this fraction to bring this v factor into the numerator and so this becomes square root 1 minus v squared over c squared over 1, after applying this exponent negative 1. Then, on the other side, we'll just write it in brackets with exponent negative 1 and leave it at that. Then we'll square both sides and the square root you can think of as bracket exponent one-half and now we are squaring that and so when you have an exponent to an exponent, you multiply the exponents and so one-half times 2 is exponent 1 and so we can write this as just 1 minus v squared over c squared. And, on the right hand side, 2 times negative 1 makes negative exponent 2. And then add v squared over c squared to both sides and also subtract this thing from both sides so well, we'll say let's move it to the left, in other words, then switch the sides around so the unknown v is on the left. So we have v squared over c squared equals 1 minus kinetic energy over mc squared plus 1 all to the negative 2 and then multiply both sides by c squared and we get this line here. And then finally take the square root of both sides. And so we have a formula for the speed of the particle which is the speed of light times the square root of 1 minus kinetic energy over mc squared plus 1 to the negative 2 and now we plug in numbers. So, we have speed of light times square root of 1 minus 0.75 megaelectron volts, which is times 10 to the 6 electron volts, times 1.60 times 10 to the minus 19 joules per electron volt so that this numerator is now in units of joules and joules is an mks unit—meters, kilograms, seconds unit— and so it works with the denominator units of kilograms and meters per second. So we are dividing by the mass of an electron and also dividing by the speed of light squared and then add 1 and take that to the negative 2 and go 1 minus this bracket and take the square root of that and you get 0.914c must be the speed of the electron to have 0.75 megaelectron volts of kinetic energy. Now, it's a very high speed and we expected that because the mass of the electron is very small—0.511 megaelectron volts— so we need the velocity to be compensatingly very high in order to make the kinetic energy, 0.75 megaelectron volts.
