Question
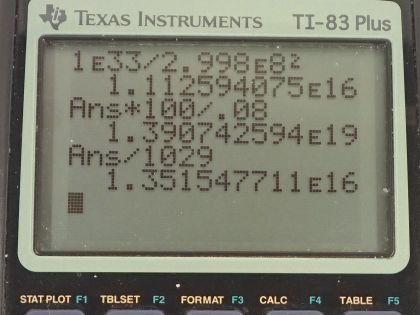
There is approximately of energy available from fusion of hydrogen in the world’s oceans. (a) If of this
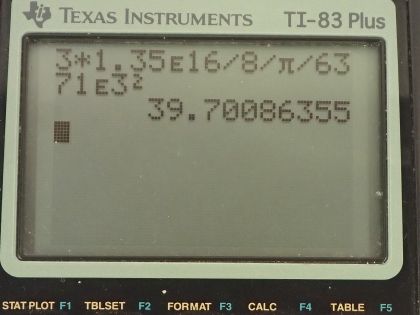
energy were utilized, what would be the decrease in mass of the oceans? Assume that 0.08% of the mass of a water molecule is converted to energy during the fusion of hydrogen. (b) How great a volume of water does this correspond to? (c) Comment on whether this is a significant fraction of the total mass of the oceans.
Final Answer
- This volume of water lost would lower sea level by approximately 40 m. Yes, this drop is significant.
Solution video
OpenStax College Physics, Chapter 28, Problem 50 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In the ocean, there's about 10 to the 33 joules of energy available from fusion of hydrogen and they might be referring to the deterium isotopes that makes up some of the water molecules when you have hydrogen that has one proton and one neutron in it and this makes heavy water... when the water is made up of hydrogen atoms that have a neutron in them. So supposing that 10 to the 33 joules of this energy was produced through fusion, how much mass would that represent? And so we rearrange this E equals mc squared formula to solve for E by dividing both sides by c squared and so we have 10 to the 33 joules divided by the speed of light squared and that's 1.1126 times 10 to the 16 kilograms. Now this is the amount of mass converted directly into energy but what the question wants to know instead though is what is the decrease in mass of the ocean? And it tells us that 0.08 percent of the mass of a water molecule is converted into energy. So the decrease in the mass of the oceans is a result of how much water mass has been used for fusion. So the change in mass of the ocean then is the amount of mass that has to be converted directly into energy multiplied by what fraction of the water molecule mass is going to get converted. So we are told that 0.08 percent is converted and this is a fraction—0.08 over a 100— and I am writing it instead as 100 over 0.08 and, you know, illustrating what these numbers represent. So for every 100 kilograms of water, 0.08 kilograms is converted into energy and here is the mass converted into energy and so converted into energy and this has units of converted into energy as well cancel and we are left with the mass of water that's going to be used. So this is basically 1 times 10 to the 19 kilograms of water and we've only one significant figure here because this is very approximate all these numbers we have involved like 10 to the 33 joules is approximate. Okay! And then how great a volume of water does this correspond to? So we have a formula for volume in terms of mass and density. So we have the mass that's used— 1.3907 times 10 to the 19 kilograms— divided by the density of sea water, which is 1029 kilograms per cubic meter and this is 1 times 10 to the 16 cubic meters. And part (c) asks is this a significant fraction of the total mass of the oceans? In order to figure out whether this is significant or not I am going to calculate the fall in sea lever that would occur if this much water were extracted from the ocean. So imagine that the ocean is a big slab and this depth is how much the sea level is going to fall the volume of this slab... this top of the slab here is going to be the area of the top multiplied by this thickness d and the area of the top, we'll take to be two-thirds the area of the Earth because about two-thirds of the Earth is covered in ocean. So the area of the Earth is the area of a sphere— 4π times the radius of the Earth squared and we multiply that by two-thirds because the oceans cover two-thirds of the area. So that's 8π radius of the Earth squared over 3 substituted in place of A and then we solve this for d by multiplying both sides by 3 over 8π radius of the Earth squared and so we have then that the depth of water that will be extracted is 3 times 1.35 times 10 to the 16 cubic meters divided by 8π times radius of the Earth squared and this works out to about 40 meters. So yes, a 40 meter drop in sea level is significant and there we go!