Question
(a) How fast would an athlete need to be running for a 100-m race to look 100 yd long? (b) Is the answer consistent with the fact that relativistic effects are difficult to observe in ordinary circumstances? Explain.
Final Answer
- A race will never be run at speeds even many order of magnitude less than that found in part (a). Extremely high speeds, not attainable for macroscopic objects on Earth, are needed to observe relativistic effects.
Solution video
OpenStax College Physics, Chapter 28, Problem 17 (Problems & Exercises)
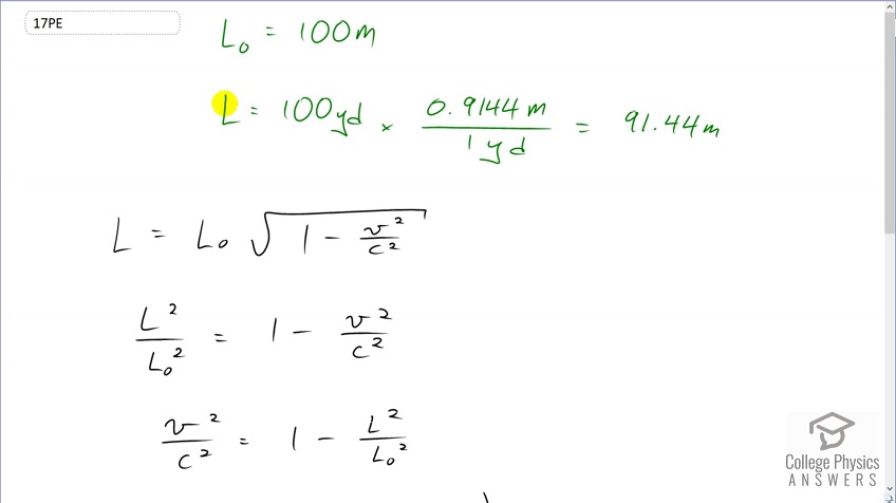
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A runner is going to be doing a 100 meter race and this 100 meters is the proper length. And then when the person is running, we are asked to figure out, what speed would they have to go so that their distance covered, appears to them, to be 100 yards instead of 100 meters? Let's convert the 100 yard into meters by multiplying by 0.9144 meters for every yard and this makes 91.44 meters. So relativistic length is going to be proper length times square root of 1 minus v squared over c squared. and then we'll divide both sides by L naught and square both sides and you have L squared over L naught squared equals 1 minus v squared over c squared. Then we'll move this term to the left by adding it to both sides and move this term to the right by subtracting it from both sides and we end up with v squared over c squared equals 1 minus L squared over L naught squared. Then multiply both sides by c squared. And we have v squared equals c squared times 1 minus L squared over L naught squared and then take the square root of both sides. So the speed then is gonna be the speed of light times the square root of 1 minus the relativistic length squared divided by the proper length squared. So that's 2.998 times 10 to the 8 meters per second—speed of light— times square root of 1 minus 91.44 meters squared divided by 100 meters squared which is 1.21 times 10 to the 8 meters per second. This is 121 million meters per second which is really really fast and no human can ever run that fast. And part (b) says, is the answer consistent with the fact that relativistic effects are difficult to observe in ordinary circumstances? And for sure because ordinary circumstances never have speeds this high and so this relativistic length contraction is not noticeable normally.