Question
The Big Bang that began the universe is estimated to have released of energy. How many stars could half this energy create, assuming the average star's mass is .
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 46 (Problems & Exercises)
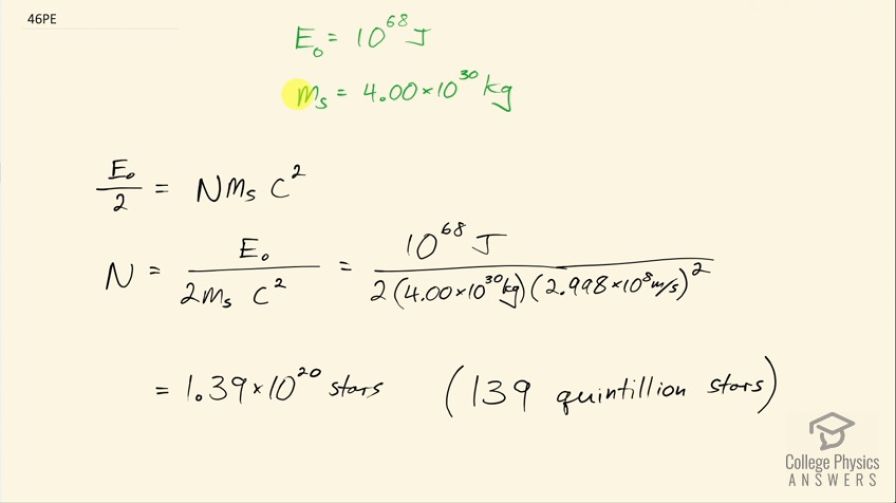
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The Big Bang of the universe released approximately 10 to the 68 joules and we suppose that the mass of a single star on average is 4.00 times 10 to the 30 kilograms and how many stars would it take to account for half of this energy? So we have that energy divided by 2 equals the number of stars times the mass per star times c squared and we have to divide both sides by m s times c squared to solve for N. So the number of stars then is the energy released by the Big Bang divided by 2 times the mass per star times c squared. So that's 10 to the 68 joules divided by 2 times 4.00 times 10 to the 30 kilograms times 2.998 times 10 to the 8 meters per second squared, which is about 139 quintillion stars.
Comments
where did N come from?
Hi Aubrey, the "N" was invented to represent the number of suns. The total mass needed is the number of suns (N, in other words) multiplied by the mass per single sun. Perhaps I could have made this more clear by writing the units of the solar mass as , which, when multipled by "suns" gives kilograms.
All the best,
Shaun


