Question
If relativistic effects are to be less than 1%, then must be less than 1.01. At what relative velocity is ?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 7 (Problems & Exercises)
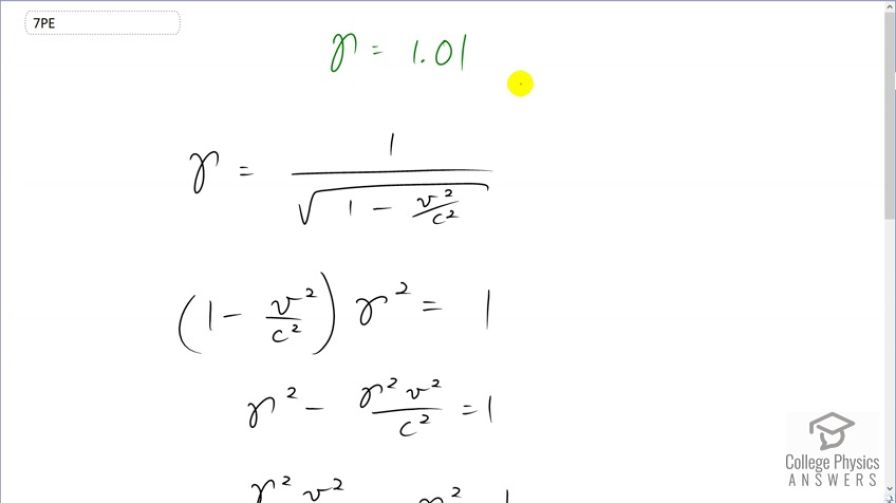
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told to assume that the Lorentz factor, gamma, is 1.01 in order that the relativistic measurement of some quantity like it's length or time is going to differ from the classical measurements by only 1 percent. So at what speed, v, will you get this gamma—1.01. So we know that the Lorentz factor is 1 over square root of 1 minus v squared over c squared and our job here is to solve for v. So we'll square both sides and then also multiply both sides by 1 minus v squared over c squared. So by squaring both sides, we end up making this this square root disappear and it turns into a bracket— 1 minus v squared over c squared which cancels with this and on the left side, we have these two things multiplied together and that equals 1 on the right side. Then we'll distribute the gamma into the brackets mulitplying gamma squared by 1 and then multiplying gamma squared by this, minus v squared over c squared as well. And then we'll add gamma squared v squared over c squared to both sides. And on the left side, it makes 0 and on the right hand side, we have 1 plus gamma squared v squared over c squared. And also the other thing I did at the same time is subtract 1 from both sides. OK. So and then switching the sides around, we have this on the left side; gamma squared v squared over c squared; on the right hand side, we have gamma squared minus 1. Then we'll multiply both sides by c squared over gamma squared in order to isolate the v squared on the left side. And then we have the next line; v squared equals c squared over gamma squared times gamma squared minus 1. And then we'll take the square root of both sides giving us v is c over gamma times square root gamma squared minus 1. So we plug in the speed of light, divide by 1.01 and then multiply by square root of 1.01 squared minus 1 giving a speed of 4.21 times 10 to the 7 meters per second. So this is the speed that an object needs in order for its relativistic values to differ from classical values.
