Question
(a) How long would the muon in Example 28.1 have lived as observed on the Earth if its velocity was 0.0500c ? (b) How far would it have traveled as observed on the Earth? (c) What distance is this in the muon’s frame?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 15 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
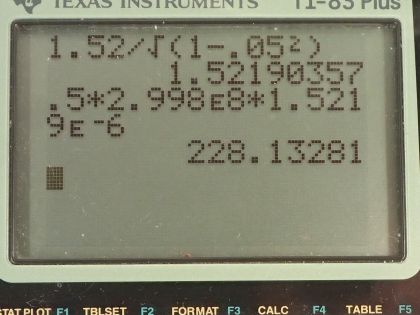
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An observer at rest with respect to a muon will measure its lifetime to be 1.52 microseconds so in other words, in the rest frame of the muon, this is its lifetime and so this is the proper time. And then suppose that the muon is going to move at a speed of 0.0500 times the speed of light c, what will its lifetime be then? Well that will be the proper time divided by square root 1 minus v squared over c squared. So that's 1.52 microseconds divided by square root of 1 minus 0.0500c all squared over c squared, the c squared's cancel leaving us with 1.52 microseconds divided by square root 1 minus 0.0500 squared, which is 1.522 microseconds. I am keeping an extra significant figure here beyond what's appropriate based on the values that we are given just to show the effect of relativity. So this is how long an Earth based observer would measure the lifetime of the muon to be— 1.522 microseconds— its lifetime is slightly dilated because the fact that it's moving past so quickly. Part (b) asks for the distance that the Earth based observer will measure for the distance that the muon will travel during its lifetime. So that's 0.0500 times the speed of light 2.998 times 10 to the 8 meters per second multiplied by the lifetime as observed by the Earth based person— this is the dilated lifetime— and that's 228.1 meters. And this is called proper length—L naught— because an Earth based observer is at rest with respect to the point where the muon comes into existence and the position where it decays so because this Earth based observer is not moving with respect to these start and end positions, the distance that they measure is the proper length. Now the distance the muon travels according to the muon, in the muon's frame, is going to be a length contraction distance L and that's going to be the proper length multiplied by square root 1 minus v squared over c squared. You could also calculate this by going L equals v multiplied by t that would be fine... or t naught I should say because this is how long the muon exists according to itself and it knows its going this speed— both frames of reference will give the same answer as to the speed— and then this would be the length according to the muon so you can try for yourself that this also will give the same answer as I am going to show here. Okay! So we have—the proper length— 228.13281 meters times square root of 1 minus 0.0500c squared over c squared, this works out to 227.8 meters is the distance that the muon will travel according to a reference frame moving with the muon or at rest with respect to the muon.
Comments
The velocity is 0.05c, so why are you using 0.5c
Isn’t the velocity supposed to be 0.05c instead of 0.5c?
Thank you so much for noticing this phoebedaramola, you're quite right. I have corrected the final answer and the calculator screenshots, and I've flagged the video for a re-do.
All the best with your studies,
Shaun
The answers are still wrong. The first calculator screenshot uses the corrected time, but still has the speed as 0.5, not 0.05. The answer should be 22.81 m and 22.78 m.
I'm slightly confused as for problem 14, you said L is the length for the earth observer, and Lo is the muon observer because that's proper time, but now it's being switched around, so I don't know which is right.