Question
(a) At what relative velocity is ? (b) At what relative velocity is ?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 10 (Problems & Exercises)
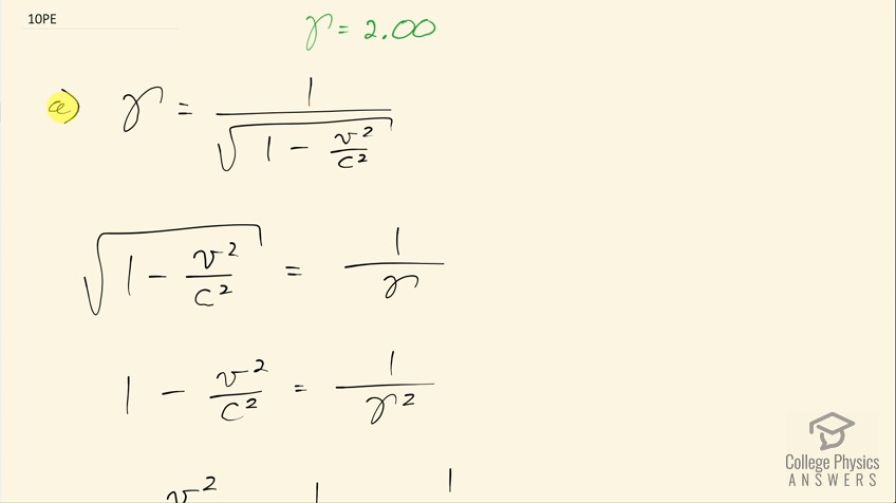
vote with a rating of
votes with an average rating of
.
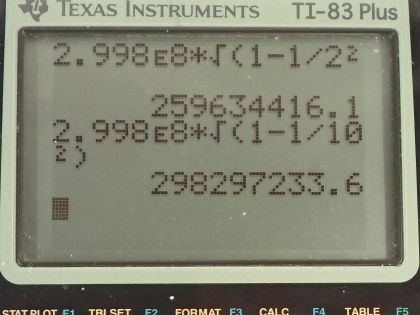
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. At what relative velocity will the Lorentz factor γ be 2.00? That's part (a) and in part (b), we'll say what speed would give a Lorentz factor of 10? So γ is 1 over the square root of 1 minus v squared over c squared, we are going to do some algebra to solve for v. First, we'll multiply both sides by 1 minus v squared over c squared and divide both sides by γ. So that gives us square root 1 minus v squared over c squared equals 1 over γ. Then we'll square both sides that gives us 1 minus v squared over c squared equals 1 over γ squared and then add v squared over c squared to both sides and subtract 1 over γ squared from both sides and you get v squared over c squared is 1 minus 1 over γ squared after switching the sides around. Then multiply both sides by c squared and you get this line here and then square root both sides and v then is the speed of light times the square root of 1 minus 1 over γ squared. That's 2.998 times 10 to the 8 meters per second times the square root of 1 minus 1 over 2.00 squared and that's 2.60 times 10 to the 8 meters per second. We can repurpose this same formula here for part (b) and we'll just plug in numbers so we have the speed v in part (b) when γ is 10.0 is going to be 2.98 times 10 to the 8 meters per second.