Question
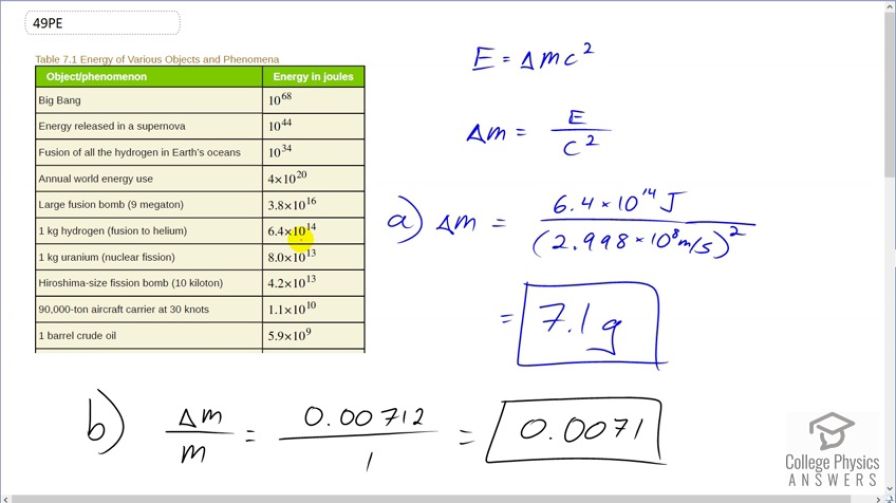
(a) Using data from Table 7.1, calculate the amount of mass converted to energy by the fusion of 1.00 kg of hydrogen. (b) What is the ratio of mass destroyed to the original mass, ? (c) How does this compare with for the fission of 1.00 kg of uranium?
Final Answer
- . The ratio of mass destroyed in fusion of hydrogen is greater than that during fission of uranium by a factor of 8.
Solution video
OpenStax College Physics, Chapter 28, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When 1 kilogram of hydrogen is fused into helium, we're told that 6.4 times 10 to the 14 joules of energy are released. And so the question is, how much mass disappears and turns into energy? So the energy released is gonna be the amount of mass that disappears times c squared. And so we'll divide both sides by c squared and we get the mass is energy divided by c squared. So the amount of mass of hydrogen that has turned into energy is 6.4 times 10 to the 14 joules of energy divided by speed of light squared which is 7.1 grams. And the fraction of hydrogen that has turned into energy is gonna be this amount of mass that's lost, which written as kilograms is 0.00712. And we divide that by the original mass of 1 kilogram, which we're told here, and that is 0.0071 so 0.7 percent has turned into energy. And then in part (c), it asks us to compare the ratio of of hydrogen that has turned into energy during fusion versus the ratio of uranium turned into energy during fission. And so this line here tells us that when 1 kilogram of uranium is fissioned, it releases 8 times 10 to the 13 joules of energy. So we have these two ratios divided by each other and the mass of hydrogen is the same as the original mass of uranium because in this table, it's 1 kilogram in each case. And so that means they cancel and we have the ΔM H over ΔM u is gonna be the energy released during the fusion of hydrogen over c squared divided by the energy released during the fission of uranium over c squared; the c squared's cancel and so we can divide these energies directly. So that's 6.4 times 10 to the 14 joules divided by 8 times 10 to the 13 joules and this gives us a factor of 8. So the ratio of mass destroyed in fusion of hydrogen is 8 times greater than the mass destroyed during the fission of uranium, which is a way of saying that fusion produces 8 times more energy per mass than fission does.
