Question
(a) What is the momentum of a 2000 kg satellite orbiting at 4.00 km/s? (b) Find the ratio of this momentum to the classical momentum. (Hint: Use the approximation that at low velocities.)
Final Answer
- to the precision limit of my calculator.
Solution video
OpenStax College Physics, Chapter 28, Problem 38 (Problems & Exercises)
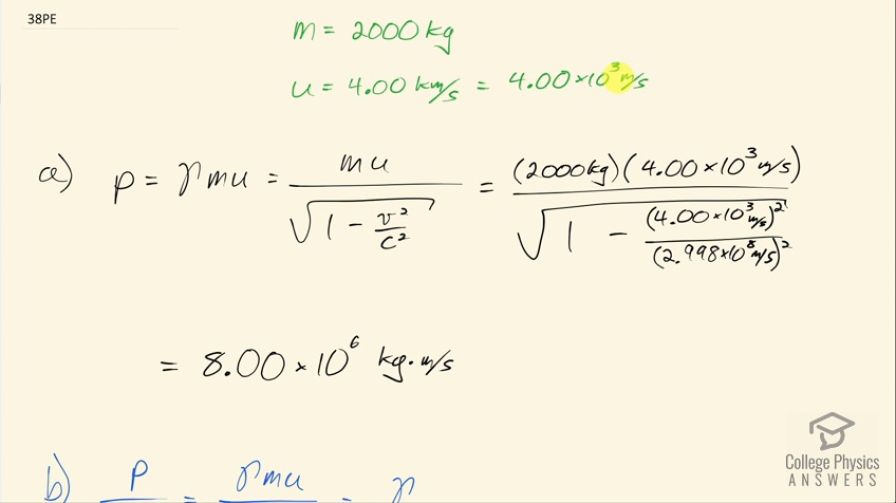
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. What is the momentum of a 2000 kilogram satellite orbiting at 4.00 kilometers per second, which is 4.00 times 10 to the 3 meters per second? The momentum is this Lorentz factor γ times the rest mass of the satellite times its velocity and that's going to be mu divided by square root 1 minus v squared over c squared when you replace γ. That's 2000 kilograms times 4.00 times 10 to the 3 meters per second divided by square root of 1 minus 4.00 times 10 to the 3 meters per second squared divided by 2.998 times 10 to the 8 meters per second squared and this is 8.00 times 10 to the 6 kilogram meters per second. Part (b) is asking us to find the ratio of this relativistic calculation for momentum to the classical calculation for momentum and the only difference is this factor γ being multiplied by mass and velocity for the relativistic version that means the mass and velocity cancels and we are left just with gamma. We are told to use this approximation for γ and I think that's because most calculators will not have enough precision in order to actually calculate what difference this would make versus just the classical case but in any case because this speed is so slow— 4.00 times 10 to the 3 meters per second— even with this approximation, we still get exactly 1 on the calculator because of the precision limit that the calculator has.
