Question
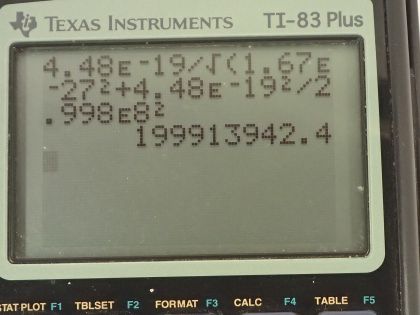
Find the velocity of a proton that has a momentum of .
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are going to calculate the velocity of a proton that has a momentum of 4.48 times 10 to the minus 19 kilogram meters per second. So the momentum is the Lorentz factor times the rest mass of the proton times its velocity and this γ is 1 over the square root of 1 minus the velocity squared over c squared so we replace γ with that and we end up with mu over square root 1 minus u squared over c squared. We are going to do some algebra to solve this for u: we will start by multiplying both sides by this square root so 1 minus u squared over c squared gets multiplied by both sides and we end up with momentum times square root 1 minus u squared over c squared equals u times mass then square both sides and we get p squared times bracket 1 minus u squared over c squared equals u squaredm squared. Then distribute the p squared into the brackets here multiplying both terms by p squared and we end up with p squared minus u squaredp squared over c squared equals u squaredm squared and then add u squaredp squared over c squared to both sides and then switch the sides around and we have u squaredm squared plus u squaredp squared over c squared equals p squared. And then factor out the u squared from both terms and we get this line here and then divide both sides by this binomial so we divide by m squared plus p squared over c squared and you get u squared is p squared over m squared plus p squared over c squared and then take the square root of both sides and you end up with this formula— it's our final step here of algebra— which is that the velocity then is the momentum divided by the square root of its rest mass squared plus the momentum squared divided by speed of light squared. So that's 4.48 times 10 to the minus 19 kilogram meters per second— momentum—divided by the square root of the rest mass of a proton 1.67 times 10 to the minus 27 kilograms squared plus 4.48 times 10 to the minus 19 kilogram meters per second squared divided by speed of light squared and that is 2.00 times 10 to the 8 meters per second.