Question
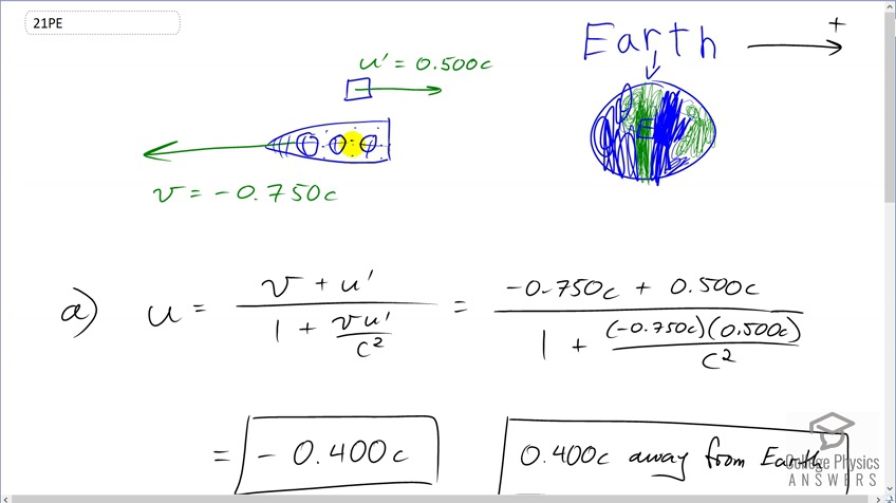
Suppose a spaceship heading directly away from the Earth at can shoot a canister at relative to the ship. (a) What is the velocity of the canister relative to the Earth, if it is shot directly at the Earth? (b) If it is shot directly away from the Earth?
Final Answer
- away from Earth
- away from Earth
Solution video
OpenStax College Physics, Chapter 28, Problem 21 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We set up our coordinate system with positive to the right and here is the Earth and we have a spaceship receding away from the Earth so it's going at a velocity of negative 0.75c because it's going to the left and we have defined to the right as positive. And it shoots a canister towards the Earth and so this is a velocity measured by an astronaut in the ship and so it is u prime because it's the velocity measured by the reference frame that is moving and we have taken the Earth to be stationary and we are saying that the spaceship is the one that's moving and so the spaceship, the reference frame that's moving, is the velocity labeled with the letter v in this relativistic addition of velocities formula. And the velocity measurement of something else by somebody in the moving reference frame is labeled u prime. And that leaves the velocity measured by somebody on the stationary reference frame is u. And so we know that u, the velocity measured, by somebody on Earth for this canister is gonna be the velocity of the spaceship plus the velocity measurement reported by somebody on the spaceship divided by 1 plus v u prime over c squared. And so the spaceship's velocity is negative 0.500c; an astronaut on the spaceship reports a velocity of positive 0.500c for the canister and that's u prime. And we divide that by 1 plus negative 0.500c times positive 0.500c over c squared. This works out to negative 0.400c and because it's negative, it's directed away from the Earth. So an Earth-based observer will notice this canister moving away from the Earth with a speed of 0.400c. And we kind of expected that because the spaceship is moving much faster to the left than the canister is moving to the right, compared to the spaceship, and so we expected a net movement to the left. OK. In part (b), we are told that everything's the same except that the canister is launched towards the left according to the observer in the spaceship. The coordinate system is the same so to the right is positive. So both of these velocities are negative then. And so the velocity measured by somebody on Earth is gonna be v, which is negative 0.750c plus negative 0.500c all over 1 plus negative 0.750c times negative 0.500c over c squared and that's negative 0.909c, which is 0.909c away from the Earth.
