Question
(a) What is the effective accelerating potential for electrons at the Stanford Linear Accelerator, if for them? (b) What is their total energy (nearly the same as kinetic in this case) in GeV?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 62 (Problems & Exercises)
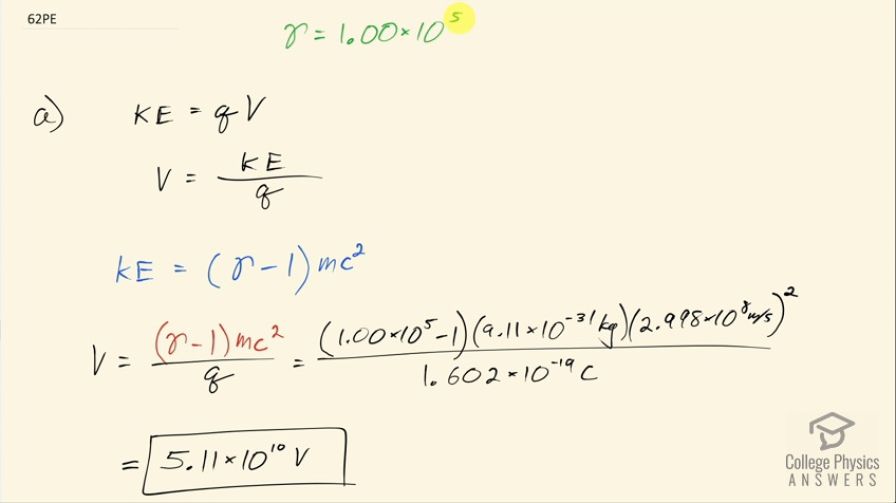
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
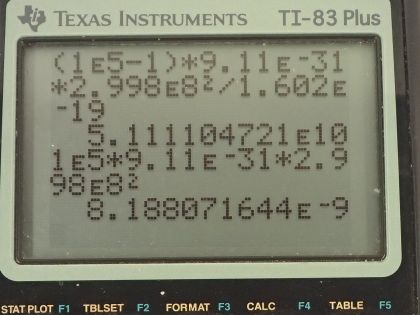
This is College Physics Answers with Shaun Dychko. We want to know what the voltage is for the Stanford Linear Accelerator knowing that γ is 1.00 times 10 to the 5 when an electron is accelerated. So the electron is going to gain an amount of kinetic energy equal to the potential energy that it looses so its kinetic energy is going to be the potential energy that it had at the beginning, which was q times V and voltage is what we are trying to solve for so we divide both sides by the elementary charge q and we can figure out what the kinetic energy is because it's going to be γ minus 1 times the rest mass energy of the electron. So we substitute γ minus 1 times mc squared in place of kinetic energy and that is 1.00 times 10 to the minus 5 minus 1 times the rest mass of an electron— 9.11 times 10 to the minus 31 kilograms— times speed of light squared divided by the charge of an electron, which is the elementary charge and that is 5.11 times 10 to 10 the volts. In part (b), what is the total energy of these particles? So that's going to be γ times the rest mass energy that's 1.00 times 10 to the 5 times the rest mass times speed of light squared and that's 8.19 times 10 to the minus 9 joules but it asks for the answer in gigaelectron volts so we multiply by 1 electron volt for every 1.602 times 10 to the minus 19 joules and then times by 1 gigaelectron volt for every 10 to the 9 electron volts and this is 51.1 gigaelectron volts.