Question
Nuclear-powered rockets were researched for some years before safety concerns became paramount. (a) What fraction of a rocket’s mass would have to be destroyed to get it into a low Earth orbit, neglecting the decrease in gravity? (Assume an orbital altitude of 250 km, and calculate both the kinetic energy (classical) and the gravitational potential energy needed.) (b) If the ship has a mass of (100 tons), what total yield nuclear explosion in tons of TNT is needed?
Final Answer
- 775 tons of TNT
Solution video
OpenStax College Physics, Chapter 28, Problem 68 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
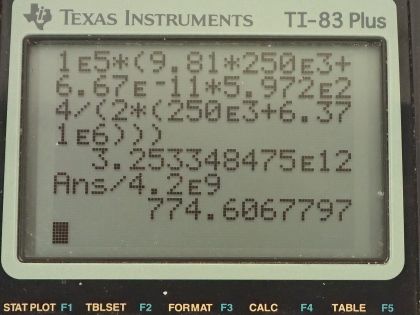
Calculator Screenshots
Video Transcript
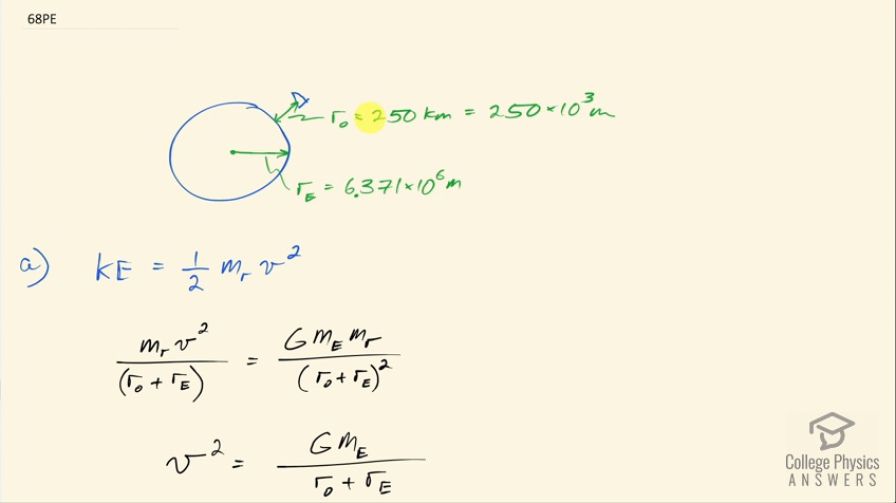
This is College Physics Answers with Shaun Dychko. A rocket is going to get launched into orbit and it has an orbital radius of 250 kilometers above the surface of the Earth and the question is what fraction of the rocket's mass, if it were to be converted directly into energy by E equals mc squared, what fraction of the rocket's mass would have to be converted into energy in order to put the rocket into this orbit? So there's going to be two types of energy that the rocket has at this position: it's going to have kinetic energy due to its motion around the Earth and it's going to have potential energy due to the increase in height above the surface. So the kinetic energy will be one-half times the rocket's mass times its speed squared and its speed we can figure out by saying that the centripetal force needed to get it going in this circle— that's m times speed squared divided by its radius of the circle— equals the force due to gravity because gravity is providing that centripetal force so that's the gravitational constant times the mass of the Earth times the mass of the rocket over the distance from the center of the Earth to the rocket squared and that distance from the center of the Earth to the rocket is the Earth's radius plus the distance from the surface to the rocket. Okay! So we can solve this for v squared by multiplying both sides by r O plus r E over mass of the rocket and so we have v squared is Gm E over r O plus r E and we are not going to take the square root of both sides here because we want v squared itself. So we are going to substitute Gm E over r O plus r E in place of v squared and we have an expression now for kinetic energy. The potential energy will be the mass of the rocket times gravitational field constant times the change in height of the rocket— that change in height is the distance above the surface, which I have labeled r O. So now the total energy then which is the amount of mass that's going to be converted into energy times c squared is going to be this potential plus this kinetic energy so now we have expressions for each of those so that's m rg r O plus m rGm E over 2 times r O plus r E. We can factor out the mass of the rocket here and so we have m r times this bracket and we want to know what fraction of mass is going to be converted into energy so we'll divide both sides by m r and also divide both sides by c squared and now we get the fraction of mass converted into energy: it's 1 over c squared times gr O plus Gm E over 2r O plus r E. So that's 1 over the speed of light squared times gravitational field strength times 250 times 10 to the 3 meters— distance from the surface to the rocket— plus the gravitational constant times the mass of the Earth, which I just looked up in a search engine divided by 2 times the distance above the surface plus the radius of the Earth and this is 3.62 times 10 to the minus 10. So a very small percentage is going to be needed to convert into energy. Now part (b) says if the ship has this mass— 1.00 times 10 to the 5 kilograms— what total yield of nuclear explosion in terms of tons of TNT is needed? So let's figure out the total amount of energy and then we look up in our data table [7.1], we have the amount of energy in joules per ton of TNT here. Okay! So we have mass of the rocket times gravitational field strength times the distance from the surface to the rocket plus gravitational constant times mass of the Earth divided by 2 times surface-rocket distance plus radius of the Earth and this works out to 3.253348 times 10 to the 12 joules and then the yield is going to be that multiplied by 1 ton of TNT for every 4.2 times 10 to the 9 joules and this works out to 775 tons of TNT.