Question
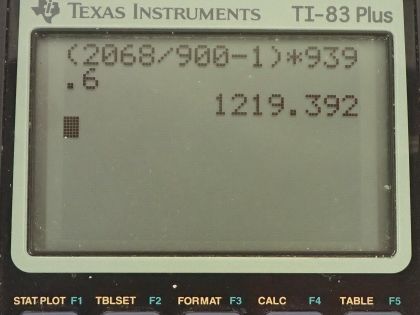
Find the kinetic energy in MeV of a neutron with a measured life span of 2065 s, given its rest energy is 939.6 MeV, and rest life span is 900s.
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 58 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A neutron has a rest mass energy of 939.6 megaelectron volts and it has a lifetime—when it's at rest— of 900 seconds and an observer watches it zip by at some speed and notices that its lifetime is actually 2065 seconds and we have to figure out what is its kinetic energy based on this discrepancy between the measured lifetime and the lifetime that it would have at rest? So kinetic energy is γ minus 1 times the rest mass energy and we also have this formula here to relate the time measured to the proper time because it's proper time multiplied by this Lorentz factor γ and so we can use this to find an expression for γ by dividing both sides by the proper time and the proper time is the time measured in the reference frame at rest with respect to what's being measured so in another words when the neutron is at rest, its lifetime is proper time. So γ then is time divided by proper time and we can substitute that in for γ here and so the kinetic energy then is 2065 seconds divided by 900 seconds minus 1 times the rest mass energy of 939.6 megaelectron volts and so its kinetic energy must be 1220 megaelectron volts.