Question
Near the center of our galaxy, hydrogen gas is moving directly away from us in its orbit about a black hole. We receive 1900 nm electromagnetic radiation and know that it was 1875 nm when emitted by the hydrogen gas. What is the speed of the gas?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 30 (Problems & Exercises)
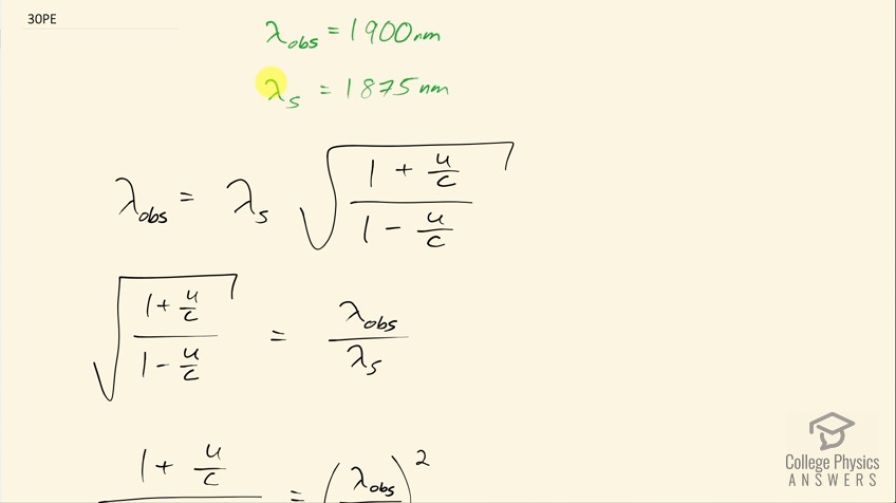
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Hydrogen that's getting sucked into the black hole at the center of the galaxy is emitting some radiation with a wavelength of 1875 nanometers according to an observer that is at rest with respect to the hydrogen. On Earth, the observed wavelength is 1900 nanometers so the wavelength has been red-shifted or it's been stretched so that means this hydrogen is moving away from the Earth and the question is with what speed is its moving away? So the observed wavelength is the wavelength emitted according to the source times the square root of 1 plus the velocity that the source is moving divided by c divided by 1 minus the velocity of the source divided by c so we are going to do some algebra here to solve for u. First thing is to multiply both sides by 1 over λ s or dividing by λ s is another way to say it and we have this line here and then we'll square both sides so we get then that the 1 plus u over c divided by 1 minus u over c is the observed wavelength divided by the emitted wavelength squared. And next step is to multiply both sides by 1 minus u over c and on the right hand side, I actually distributed the λ obs over λ s squared into the brackets here so we have λ obs over λ s squared minus this fraction times u over c and on the left side, we have 1 plus u over c. We need to collect the terms together to have the letter u in them and we'll do that by first subtracting 1 from both sides so that brings the 1 to the right and then we'll add λ obs over λ s squared times u over c, this term will get added to both sides so it's probably easier to copy this and move it over here so it's being added to both sides. So we have on the left side then u over c plus this term equals this fraction squared minus 1. Then factor out u over c from both terms on the left so we have u over c times 1 plus λ obs over λ of the source squared equals λ obs over λ source squared minus 1. Then multiply both sides by c and divide both sides by this bracket here so dividing by 1 plus λ obs over λ s squared and that's happening to both sides and so we get this line here— we have a formula now for the velocity of the source given the wavelength that's observed— and the wavelength that we know is being emitted. So we have 2.998 times 10 to the 8 meters per second—speed of light— times 1900 nanometers—wavelength observed— divided by 1875 nanometers—that we know was emitted—squared minus 1 divided by 1 plus that ratio squared and this is 3.97 times 10 to the 6 meters per second must be the velocity with which the hydrogen gas is moving away from the Earth.
