Question
A -meson is a particle that decays into a muon and a massless particle. The -meson has a rest mass energy of 139.6 MeV, and the muon has a rest mass energy of 105.7 MeV. Suppose the -meson is at rest and all of the missing mass goes into the muon’s kinetic energy. How fast will the muon move?
Final Answer
Solution video
OpenStax College Physics, Chapter 28, Problem 52 (Problems & Exercises)
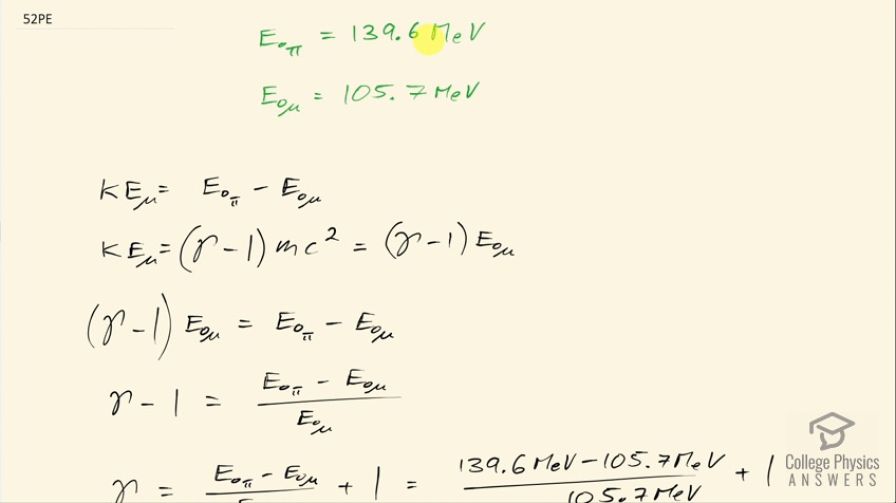
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
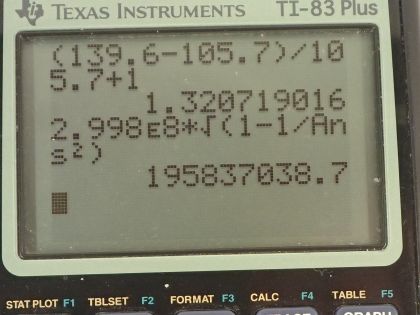
This is College Physics Answers with Shaun Dychko. A pi meson with a rest mass energy of 139.6 megaelectron volts decays into a muon and another mass-less particle, which is a neutrino and the question is asking assuming that this pion is initially at rest, how fast will this muon be traveling assuming that this missing energy because there's a difference in the rest mass energy of these two particles... assume all that missing energy goes into kinetic energy of the muon. So the kinetic energy of the muon then is this difference between the rest mass energy of the pion and the muon and we know kinetic energy is also this Lorentz factor γ minus 1 multiplied by the rest mass energy of the particle and so that's a muon so I can substitute mc squared with E naught μ. Okay! Now we can equate this with this then which we do on this line and then divide both sides by the rest mass energy of the muon and we get this line here, add 1 to both sides and we have an expression for γ and in order to make our algebra a little simpler, I am going to actually evaluate what this is instead of carrying this expression forward into the work down here in solving for speed given γ. So we have 139.6 megaelectron volts— rest mass energy of the pion— minus 105.7 megaelectron volts— rest mass energy of the muon— divided by the muon's rest mass energy plus 1 and that's 1.320719; keeping lots of digits there because this is an intermediate calculation and we don't want to have intermediate rounding error. So the Lorentz factor is also 1 over the square root of 1 minus the speed squared of the particle divided by speed of light squared so we are going to solve this for v. First we'll square both sides so we have γ squared equals 1 over 1 minus v squared over c squared and then multiply both sides by 1 minus v squared over c squared divided by γ squared so that's on both sides. So on the left, we have 1 minus v squared over c squared and on the right we have 1 over γ squared. Then we'll add v squared over c squared to both sides and subtract 1 over γ squared from both sides then we have this line here after switching the sides around. So we have v squared over c squared equals 1 minus 1 over γ squared then multiply both sides by c squared and you have this line here square root both sides and you have v then is the speed of light times the square root of 1 minus 1 over γ squared. So that's 2.998 times 10 to the 8 meters per second times the square root of 1 minus 1 over γ squared— and γ has no units by the way— so that's 1.958 times 10 to the 8 meters per second.